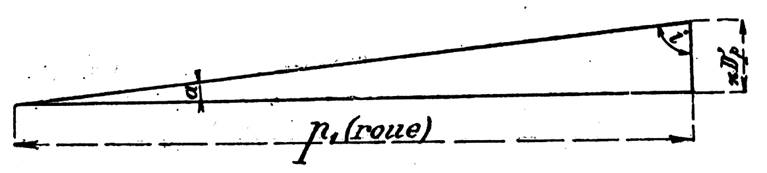Index warmaths								Liste des cours sur la trigonométrie.
APPLICATIONS : LES RELATIONS TRIGONOMETRIQUES .
Champ d’application  1 : LES FORCES en mécanique.
1°) Un corps est soumis à l’action de deux forces concourantes ,, l’une de 1650 N l’autre de 3250 N . Ces forces font entre elles un angle de 56° 25’ . Calculer la valeur de la résultante des deux forces ainsi que son inclinaison par rapport aux deux composantes.
2° ) On veut remplacer l’action d’une force de 900 N par celles de deux forces ayant même point d’application que la première . L’une des deux forces est connues et vaut 380 N ; l’angle qu’elle fait avec celle de 900N est de 19° 20’ . On demande de calculer l’intensité de la deuxième force ainsi que l’angle des composantes.
Champ d’application 2  : Travaux de dessin et d’atelier -
Ce document vous montre des applications des relations trigonométriques. Et des problèmes à résoudre………… !
A ) Applications de la pente d’une droite ou d’un plan : Clavettes et cônes
Problème 1 :
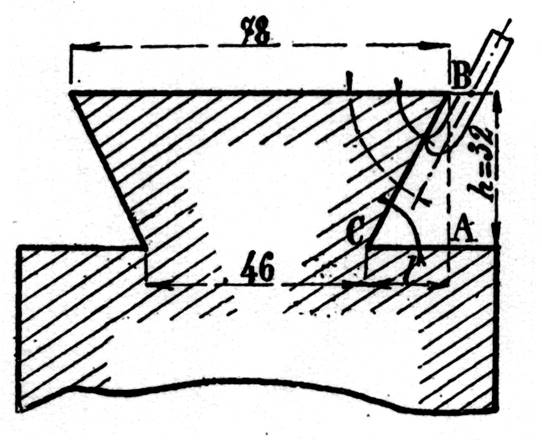
Etant donné le croquis ci contre d’une clavette transversale, calculer la pente des faces inclinées et l’angle « a » formé par ces deux faces. ( pente = 1/25 ou 4%) ; ( a = 2 i = 4° 34’)
Problème 2
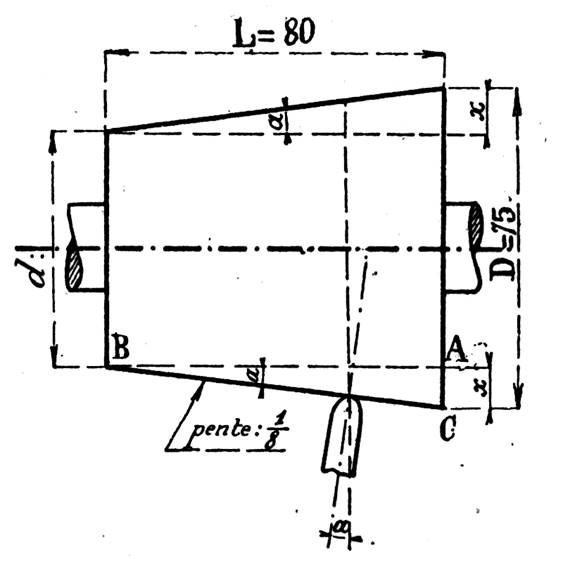
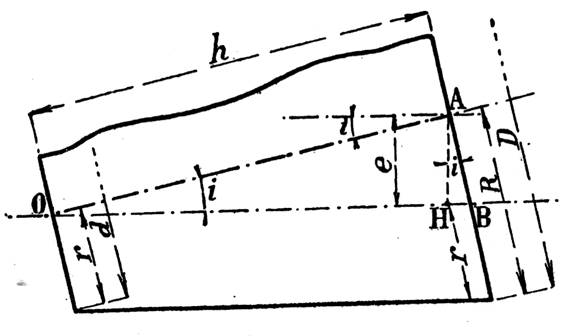
: Calculer la dimension de « x » de la clavette à talon donnée par le croquis ci dessous. ( x = 6 mm ; AB = 4 mm)
Problème N°3 :
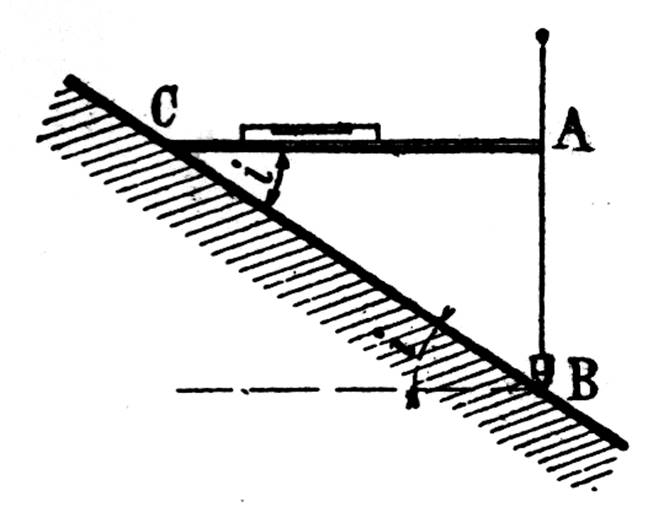
Soit la figure ci contre : Trouver la pente d’un plan incliné au moyen du niveau à bulle d’air. Si AB = 0,75 m et AC = 1,20 m (Pente = 5/8 ou 0,625 )
Problème 4 :
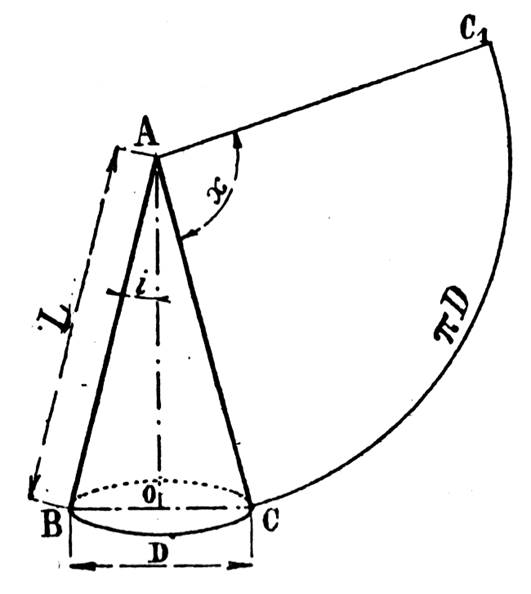
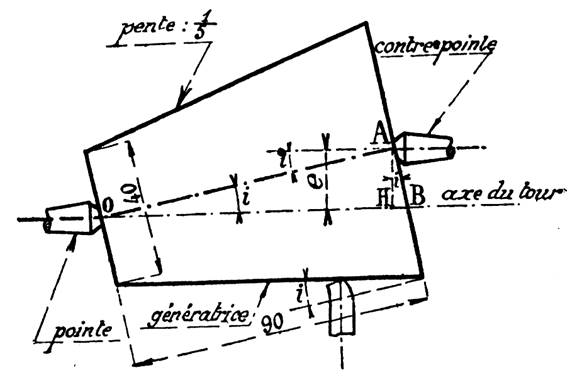
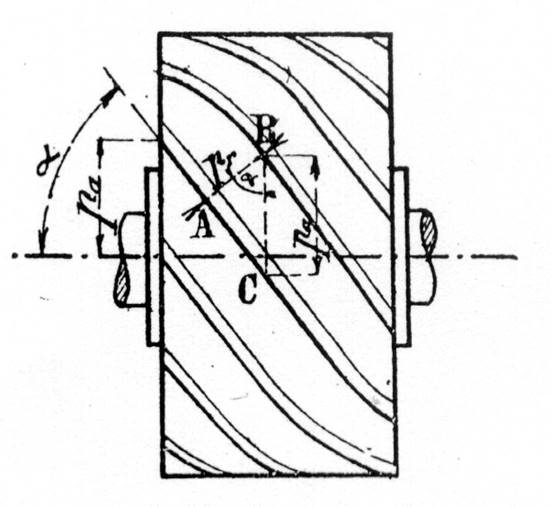
Calculer l’angle du secteur angulaire donnant après enroulement un cône d’angle au sommet « 2i ». ( x = 360° sin i )
PB n° 5 : application numérique : calculer l’angle du secteur circulaire capable du cône de 30° au sommet. ( x = 93° 15 ‘ par excès)
Problème n°6 .
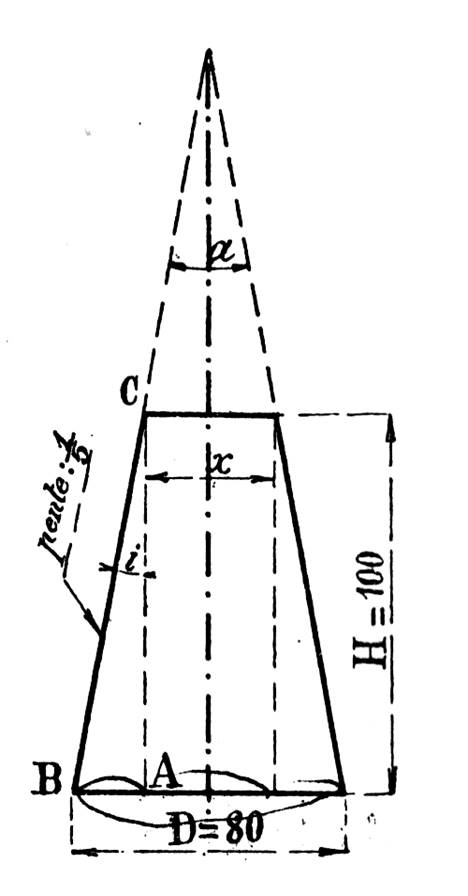
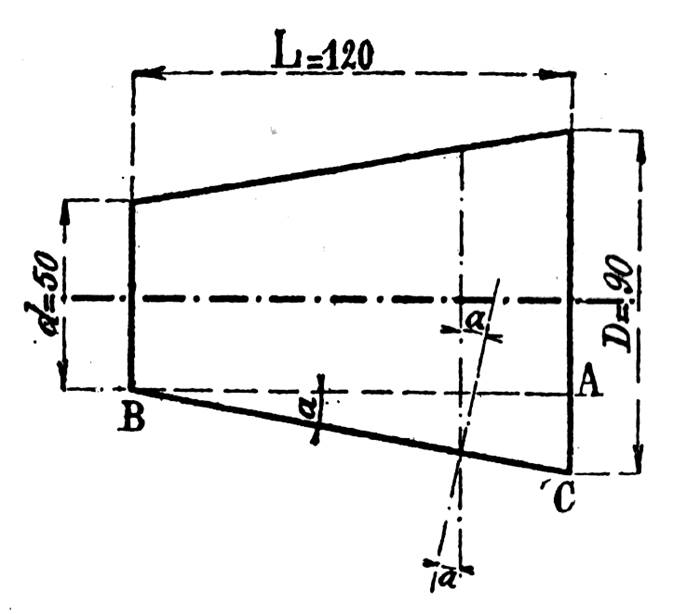
Calculer l’angle au sommet « a » du cône donné par le croquis ci contre, ainsi que le diamètre du tronc de cône. ( x = 40 mm)