|
Niveau V LECON N°24 |
Devoir : Ÿ Remédiation : Ÿ |
Nom :…………
|
Classe : Groupe : |
|
|
Date :…………… |
Rattrapage : Ÿ Soutien : Ÿ |
Prénom :…………
|
Note
contrôle : |
Note
évaluation : |
|
|
- Donnez l ’ équation type (modèle mathématique) représentant la
fonction affine
- Que peut-on représenter à partir d'une équation représentant la fonction affine ?
- Soit la notation « a x + b »
, comment nomme - t - on « a » ; « x » et
« b » ?
- Donnez la forme des couples qui forment eux mêmes le graphe de la
fonction affine
.
- Donner les deux couples caractéristiques qui forment le graphe de la fonction
affine
.
- Représenter le tableau de variation de la
fonction affine; précisez ce qu’il « contient ».
- Définissez
« la représentation
graphique » de la fonction affine;
- précisez ,(en citant les caractéristiques
principales et les placer dans
un repère cartésien.)
- De combien de façons peut-on reconnaître une fonction dite « affine » ?
EVALUATION :
Série 1
EXERCICES :
Sachant que les tableaux
suivants correspondent à des
applications affines, les compléter .
1°) donner l’expression
permettant de calculer f(x) connaissant « x » ( « a »
= 2 pour le premier tableau).
|
-4 |
-3,5 |
-1,25 |
0 |
1 |
2 |
4 |
6 |
|
|
f(x) |
|
|
|
-3 |
|
|
|
|
2°) donner l’expression
permettant de calculer f(x) connaissant « x ».
|
x |
-5 |
-3 |
-1,5 |
0 |
1 |
2 |
5 |
|
f(x) |
|
|
|
1,5 |
0,5 |
|
|
Série 2
Problème
1 : Dans un
repère cartésien , construire les points A de
coordonnées ( 1 ; - 0,5 ) et B de
coordonnées ( -2 ; 9 ) . Tracer la droite (AB).
Construisez le point de
cette droite d’abscisse 2 . Quelle est son
ordonnée ?
Quelle est l’ordonnée du
point d’abscisse x = 0 ?
Quelle est l’abscisse du
point d’ordonnée y = 0 ?
Quelle est l’équation de la
droite ( AB) ?
Problème 2 :
Représenter graphiquement dans un repère
cartésien les applications affines définies par les relations
.
|
y= |
y= |
y= x - 1,5 |
Problème 3 :
Représenter graphiquement
dans un repère cartésien les
applications affines suivantes :
y1 = 2x – 3 ;
y2 = -0,75 x + 3,25
On constate que les deux
droites représentatives de ces deux applications affines sont concourantes en
un point M.
Donner graphiquement les
coordonnées du point M.
Problème 4 : Représenter graphiquement dans un repère cartésien
les deux applications suivantes : y1 = ![]() x ; y2 =
x ; y2 = ![]() x -3
x -3
Quelle remarque pouvez-vous
faire sur ces deux droites représentatives ?
INTERDISCIPLINARITES
|
Problème 1 : Une automobile possède un réservoir de 65
litres. Au départ d’un voyage , il fait le plein et le compteur journalier est
mis à zéro. L’automobile consomme 9
litres de carburant aux 100 km . « x » désignant
le nombre de km parcourus et f(x) le
nombre de litres de carburant restant , donner l’expression permettant de calculer f(x)
connaissant « x » . Construire sa
représentation graphique ; 1 cm en abscisse représentant 50 km et 1 cm
en ordonnée représentant 5 litres de carburant. Quelle distance maximale
peut-il parcourir avec un plein du réservoir ? Le réservoir est rempli au
quart ; quelle distance peut-il
espérer parcourir ? |
|
Problème 2 : Un carré a pour côté 1,5 cm . On augmente son côté d’une longueur « x ». Calculer
le périmètre de ce nouveau carré. Désigner par f(x) ce périmètre. Montrer que l’application
est affine. Préciser les coefficients « a » et « b ». Construire sa
représentation graphique pour « x » compris entre 0 et 4 , en cm |
|
Problème 3 : Soit un secteur angulaire
droit [ Ox ; Oy] Placer le point A de la
demi-droite [Ox) et le point B de la demi- droite [Oy) tels que OA = 60 mm et OB = 80 mm. 1°) en utilisant la
relation de Pythagore, calculer la longueur AB . 2°) Soit un point M quelconque
de la demi-droite [ Ax) .
mener par M la parallèle à la droite ( AB) . Elle
est sécante en P à la demi-droite [Oy). En utilisant la propriété de Thalès ,
calculer , en fonction de « x »
, les longueurs AM , MP , BP. 3°)Exprimer
, en fonction de « x », le périmètre du trapèze AMPB.
Vous désigner cette expression par f(x). Montrer que l’application
« f » est affine. Préciser ses coefficients. Construire sa
représentation graphique. Déterminer la position du
point M pour laquelle le périmètre est égal à 300mm. |
|
Problème 4 : Une pièce cylindrique a
pour diamètre D = 20 mm. On enlève au tour une
quantité de métal et le diamètre de
« x » mm. Quel est son nouveau
diamètre en fonction de « x » ? Donner l’expression
permettant de calculer f(x) , longueur du cercle de
la section , connaissant « x ». Montrer que l’application « f » est
affine. Préciser les coefficients « a » et « b ». Construire sa
représentation graphique pour « x » compris entre 0 et 5 , en mm. |
|
Problème 5 : Pour déposer des plis
urgents on fait appelle à un taxi . Le prix d’une course d’un
taxi se compose : -
de
la prise en charge : 2,1€ -
d’une
somme calculée suivant le nombre de kilomètres parcourus : 0,8 € par km. Combien
doit-on payer pour aller en A à 2 km
de son point de départ ( PA)? Quelle somme doit-on payer
en plus de PA pour aller en
C situé à 5 km de A ? Exprimer de même PC en fonction de PB ( B et C sont distant de 3 km). Exprimer
le montant p(x) d’une course de « x » kilomètres. Quelle est la nature de
l’application qui , au nombre de kilomètres associe
le prix de la course ? Faire la représentation
graphique ; en « x » le nombre de kilomètres ( 1 km :2 cm) en « y » le prix de la course
( 1€ = 2 cm) |
|
Problème 6 : Un pépiniériste propose une
promotion sur ses arbustes à fleurs. Moyennant un forfait de 10 € pour le transport , quelle que soit la distance , il livre ses
arbustes au prix de 9,2 € la touffe. Etablir la relation
mathématique de la forme
« affine » et calculer la dépense pour les achats suivants : a)
3
lilas et 5 forsythias. b)
7
cytises. c)
4
boules de neige et 9 berbéris. d)
3
aubépines roses. 6 noisetiers pourpres. |
|
Problème 7 : Un artisan doit faire livrer
ses produits dans un rayon de 350 km autour de chez lui .Il a reçu les offres
de deux transporteurs aux conditions suivantes : Transporteur A : 2,3
€ du kilomètre. Transporteur B : 120
€ de forfait et 1,1 € par km . a)
construire
dans un même repère les représentations graphiques des coûts pour
« x » km correspondants aux deux propositions. b)
Quel
est le transporteur le moins cher pour 20 km ? pour 350 km ? c) Indiquer
, suivant la valeur de « x » , l’expression du coût
minimum en fonction de
« x ». |
|
Problème 8 : Une personne achète une
voiture dont le prix de vente est 10450 €. Pour le règlement
, le vendeur lui propose deux solutions/ 1ère
solution : en payant comptant , le vendeur
accorde une remise de 3% sur le prix de vente de la voiture. 2ème
solution : si le payement à lieu à crédit , le
règlement s’effectue ainsi : -
à
la commande 1045 € , -
le
reste majoré de 20 % en 48 mensualités. 1°)Quel
est le prix payé en choisissant la première solution ? 2°)Quel
est le montant d’une mensualité pour la 2ème solution ? 3°)Quel
est le prix final de la voiture si on paie à crédit ? |
|
Problème 9 (voir graphique) Deux flacons contiennent
des liquides différents qui s’évaporent peu à peu. Sur le graphique
, on représente en fonction du nombre de jours d’évaporation la
hauteur en millimètres du liquide restant dans le premier flacon par le
segment [AB]. On représente de même en
fonction du nombre de jours d’évaporation la hauteur en millimètres du
liquide restant dans le deuxième flacon par le segment [KL]. 1°) pour le premier
flacon, en utilisant ce graphique : a)
lire
la hauteur du liquide en début d’expérience. Donner ce résultat. b)
Lire
le nombre de jours nécessaires pour que tout le liquide soit évaporé. Donner
ce résultat. c)
Vérifier que les points A et B appartiennent
à la droite d’équation x + 4y – 24 = 0 2°) En utilisant le graphique , déterminer au bout de combien de jours les
deux liquides ont la même hauteur dans les deux flacons. |
|
|
|
Problème 10 Le physicien Albert
Einstein a prouvé en 1920 que le temps ne s’écoulait pas toujours de façon
identique. Ainsi des astronautes voyageant dans un vaisseau
spatial presque aussi rapide que la lumière , disons 250 000 km / s , vieilliraient moins
vite au regard de leur amis restés sur terre. Si « A » est
leur âge au départ , si « t » est le temps
qui s’écoule sur terre et si
« Av »est l’âge des voyageurs , on a la relation : Av = 0,3 t
+ A L’un d’eux est parti en
l’an 2000, il avait 20 ans . 1°) Quel âge aura –t-il en
2010 ; en 2020 ? 2°) A quelle date aura t-
il 25 ans ? 3°) Il a laissé en partant
un enfant tout juste né. Qu’en sera-t-il quand il reviendra âgé lui-même de
30 ans ? |
|
|
|
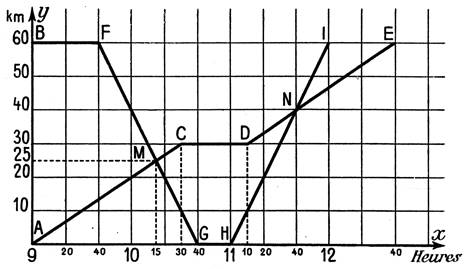
11°) Interprétez les
tracés ci dessous. Début de l’histoire :
Un véhicule se trouve
en « A » ; un autre véhicule se trouve en B : ………………. ( Raconter l’histoire
de ces deux véhicules…….) |
|
|