CORRIGE : Objectif: Détermination de l’équation d’une droite de la forme
« y = a x +b ».
|
|
CONTROLE |
|
1°)
Donner la procédure qui permet de déterminer l'équation d'une droite dont on connaît le coefficient directeur et un
point de la droite.
On connaît « a », il suffit de déterminer « b »
La droite passe par le point A ( x1 ; y1) ;
on a y1 = a x1 + b
On en déduit la valeur de « b » : b = y1 - a x1
(le calcul terminé , il suffit de remplacer « b » dans
l’équation de départ par la valeur
trouvée)
2°) Donner une procédure qui permet de déterminer l'équation d'une droite dont on connaît deux couples de nombres.
Procédure :
1°) On calcule « a » : tel que ![]()
2°) on se fixe (choisi) un point
« A » ou « B » , on prend ses coordonnées
3°) On connaît « a », il suffit de déterminer
« b »
La droite passe par le point A ( x1 ; y1) ;
on a y1 = a x1 + b
On en déduit la valeur de « b » : b = y1 - a x1
(le calcul terminé , il suffit de remplacer « b » dans
l’équation de départ par la valeur
trouvée)
3°)
Donner l’équation générale de la droite.
4°)
dans l’équation générale de la droite :
Quelle conclusion faut-il tirer sur la représentation graphique ?
a) « a » = 0 et « b » ≠ 0
b)
« a » ≠ 0 et « b » = 0
c)
« a » ≠ 0 et « b » ≠ 0
|
|
|
N°1 :
Déterminer
l’équation de la droite de coefficient directeur « -0,5 » et passant
par le point A ( 4 ; -1) ; à
vérifier par le tracé.
L’équation est de la forme y =
a x + b ,
Puisque
« a » = -0,5.
Soit y = - 0,5 x + b (1)
Nous avons les coordonnées de
A « x » = 4 ;
y = -1
On remplace dans l’équation (1) :
-1 = 0,5 fois 4 + b
soit -1 = -2 + b
d’où après transformation : « b » = 1
en conclusion :
l’équation cherchée est y = -
0,5 x + 1
( à vérifier par la résolution graphique)
N
°2 :Déterminer l
’équation de la droite passant par les points A ( -2 ;1) et B ( 3 ;
3) ; à
vérifier par le tracé.
1°) on calcule « a » : ![]()
2°) L’équation est de la forme y = a x + b
y = 0,4 x
+ b
3°)
d’après l’ énoncé ,en « A »
pour x = - 2 nous devons
avoir y = 1
1 = 0,4
fois (-2) + b
1 = - 0,8
+ b
1 + 0,8 = b
d’ où b = 1,8
4°) L’équation cherchée est y = 0,4 x + 1,8
Nota : on aurait pu prendre les
coordonnées du point « B »,
nous serions parvenu au même résultat. (à vérifier par le graphique)
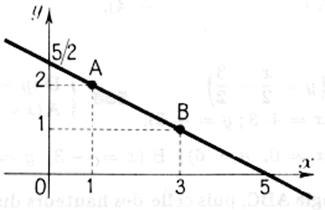
N° 3 Déterminer l'équation de la droite
définie par deux points A ( 1 ; 2 ) et B
( 3 ;1 ) ; à vérifier par le tracé. .
|
|
|
|
|
|
l'équation est de la forme y =
a x + b .
Ecrivons que les
coordonnées de A ;puis celles de B , vérifient cette équation .
Nous obtenons :
Pour A ( x = 1 et y = 2 ) ;
nous obtenons : 2 = a ![]() 1 + b
;soit (1) a + b = 2
1 + b
;soit (1) a + b = 2
Pour B ( x = 3 et y = 1 )
: nous obtenons : 1 = a ![]() 3 + b
; soit ( 2) 3a + b = 1
3 + b
; soit ( 2) 3a + b = 1
Les relations ( 1) et
(2) représentent la même équation ; elles permettent de
calculer "a" et "b"
Commentaire : Nous sommes en présence d’un système de deux
équations que l’on décide de résoudre par la méthode de l’addition.( voir résoudre le système de (1) et (2) )
soit le système : ![]() ;
;
pour
résoudre ce système on décide de multiplier
« a + b = 2 » par -
1 , on peut ainsi remplacer dans le système « a + b = 2 » par
« - a - b = - 2 »
nous avons le nouveau système : ![]()
on additionne terme à
terme dans les deux membres :
3a - a = 2a ; b -
b = 0 ; 1 - 2 = -1 ;
Le résultat de l’addition des deux
équations terme à terme nous donne
donc 2a +0 = -1
on
en déduit que « a » = ![]() ou a = - 0,5
ou a = - 0,5
on en déduit b = ![]() = 2,5;
= 2,5;
L
équation de la droite AB est donc : ![]() ou y = - 0,5 x + 2,5
ou y = - 0,5 x + 2,5
N°4 : soit le tableau suivant :
|
Température « x » moyenne extérieure ( °C) |
-
5 |
-3 |
0 |
5 |
10 |
|
Consommation « y » de fuel / 24 h ( l ) |
38 |
36 |
32 |
25 |
18 |
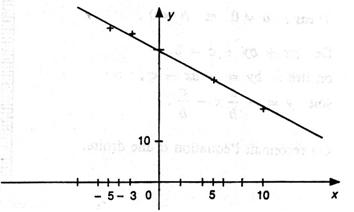
Représenter le nuage des points M ( x ; y )
Ajuster une droite . Donner son équation.
En déduire la consommation à prévoir si la
température se maintient à - 10 °C pendant 5 jours.
Solution :
|
|
|
D’ où y = - 1,35 x + 31,70
Si la température se maintient à - 10 °C
pendant 5 jours, il faut envisager une consommation de 5 ( 13,5 + 31,70 ) » 226 , soit 226 litres.