|
|
CONTROLE . |
.DOSSIER N°22 |
|
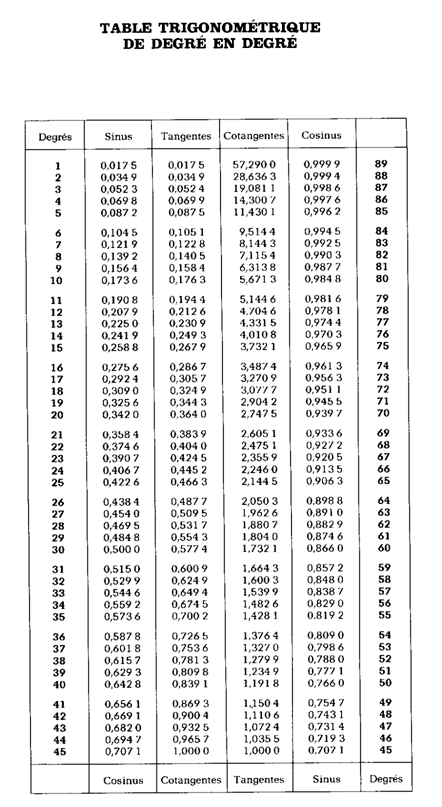
Le sinus de 36° (0,5878) est égal au cosinus de 54°
|
||
|
Leçon |
Devoir de rattrapage. |
|
||||||
|
N°22 |
LES RELATIONS TRIGONOMETRIQUES DANS
LE TRIANGLE RECTANGLE |
|
||||||
|
|
|||||||||
|
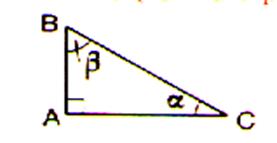
1°) Les angles ( désignations) . Mots à placer : AC. ( ou CA ) ; l’angle droit ; côté
adjacent ; Bêta ;
alpha ; AB ( ou BA ) ;
consécutifs. |
|||||||||
|
Pour le symbole « b » lire « …….. » Pour le symbole « a » lire « ……… »
En « A » : un carré (ou rectangle) symbolise ……………….. |
|
||||||||
|
L’angle
« b » se trouve à
l’opposé du côté ………. ( ou ……) L’angle
« a » se trouve à l’opposé du côté …….. ( ou ………. ) Les côté AB et BC sont ……………. ;
. ( AB est appelé le « ……………… »
à l’angle « b ») Les côtés AC et CB sont ……………..
( AC est appelé le « ……………….. » à
l’angle « a ») |
|||||||||
|
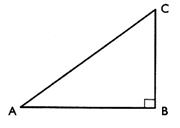
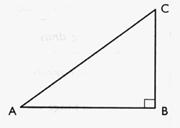
2°) Identification du « Côté opposé » ,
« côté adjacent » , « hypoténuse » d’un angle Pour un triangle rectangle CBA ; rectangle
en B :nommer les côtés :
Compléter le tableau suivant avec les mots :
Côté opposé ( à |
|||||||||
|
|
Si l’on se fixe sur un angle ; on nommera les côtés de la façon suivante : |
||||||||
|
|
Pour l’angle droit |
Pour l’angle |
Pour l’angle |
||||||
|
AC est appelé : |
|
|
|
||||||
|
AB est appelé |
|
|
|
||||||
|
BC est appelé |
|
|
|
||||||
|
3°) citer
les 3 principales relations trigonométriques sur le sinus , cosinus ,
tangente ; donner le modèle symbolique
mathématique. 4°) Appliquer
au triangle rectangle ACB les relations précédentes :
A quel rapport est égal ? :
5°) Passage d’une valeur décimale d’un sin a; cos a, tan a, à la valeur en
degré de l’angle a Compléter les phrases suivantes :avec les
mots : en degré ; valeur
décimale . Lorsque l’on connaît la valeur décimale du sinus
, du cosinus ou de la tangente d’un angle ,en consultant une table
numérique ou une calculatrice
scientifique obtenir la valeur …………………… de cet angle . Inversement si je connais la valeur en degré de
l’angle je peux obtenir avec la table numérique ou la calculatrice la
……………….. du sinus , cosinus
ou tangente de cet angle .Le chapitre suivant aborde ce
travail. 6°)
Détermination de la valeur décimale d’un sinus , cosinus et tangente à
partir de la valeur en degré de
l’angle aigu. Compléter les phrases suivantes : Avec les mots suivants :« grades ; degré
décimal ; la calculatrice , degrés décimaux , ou radians . DEGRE ;ou une table
numérique » Les valeurs des rapports trigonométriques ( sinus
, cosinus , tangente ) d’un angle aigu sont données par ……………………………………………….. Sur une calculatrice , les angles peuvent être
exprimés en :………………………..……………………………………………………….. L’unité d’angle utilisé couramment est le …………………………………... 7°) pour des calculs en trigonométrie il
faut mettre la calculatrice en mode……… 8°)
Compléter le tableau ( voir votre calculatrice) |
|||||||||
|
Pour trouver le sinus d’un angle aigu |
Introduire la mesure de
l’angle ( en degré) |
Puis presser sur la touche …………… |
|||||||
|
Pour trouver le cosinus d’un angle aigu |
Introduire
la mesure de l’angle ( en
degré) |
Puis presser sur la touche ……………… |
|||||||
|
Pour trouver la tangente sinus d’un angle aigu |
Introduire
la mesure de l’angle ( en
degré) |
Puis presser sur la touche ………………….. |
|||||||
|
8°) mettre la calculatrice en mode DEGRE |
|||||||||
|
Détermination de la valeur de l’angle en degré connaissant la valeur du sinus ou
cosinus ou tangente avec la calculatrice : Donner la touche remplissant la même fonction sur votre calculatrice : A
partir de la valeur décimale
« sinus » pour obtenir la
valeur en degré appuyer sur la
touche : INV . SIN ; ou SIN-1 ;
ou ASN ; A partir
de la valeur décimale
« cosinus » pour obtenir la
valeur en degré appuyer sur la
touche INV . COS ; ou COS-1 ; ou ACN ; A partir
de la valeur décimale
« tangente » pour obtenir la
valeur en degré appuyer sur la
touche INV . TAN ; ou TAN-1 ; ou ATN ; |
|||||||||
|
9 °)
Utiliser la calculatrice pour trouver
l’angle C dont le sinus est 0,876 5 , l’angle
A dont le cosinus est 0,423 6
et l’angle C dont la
tangente est 1,973 2 10 °)
Compléter les phrases suivantes sur les Calculs d’éléments d’un triangle
rectangle :
avec les mots : « 180° ; aigus ;
Pythagore ; complémentaires ;( somme des 2 angles aigus) . »
a) Dans un triangle rectangle si l’on connaît
2 côtés on peut avec « …………… » trouver la longueur du troisième
coté . b) La somme des angles dans un triangle est
de …………. . …………………… c) La somme dans un triangle rectangle est
de …… = 90° + ………………………..(ces deux
angles aigus ,dont leur somme est de 90°, sont appelés :
angles ……………………….) d) Dans un
triangle rectangle , si je connais la longueur de deux côtés , j’applique …………………. trouver la longueur du troisième
côté. e) Dans un triangle rectangle , si je connais
la longueur de deux côtés , je
peux calculer le sinus ou
le cosinus ou la tangente pour
trouver la valeur d’un des angles
« ………………» |
|||||||||