|
Voir leçon |
TRAVAUX d ’ AUTO - FORMATION sur |
|
N°11 |
CORRIGE
PROBLEMES DU PREMIER DEGRE |
( vous devez vous aider du cours !!!!!)
|
EXERCICES : Mettre en équation et résoudre. (on pose « x » l’inconnue) |
|
|
N°1 :La moitié d’un nombre vaut 18 . Quelle
est la valeur de ce nombre ? |
|
|
a)
On désigne ( remplace) le mot « nombre » par la lettre
« x » . L’énoncé
devient : La moitié de « x » vaut 18 ou
La moitié de « x »
égale 18 b) On traduit par l’équation : c)
Résoudre :
( « résoudre » une équation du premier degré c’est
rechercher la valeur de « x » , qui remplacer dans le premier
membre , après calcul , vérifie « l’égalité vraie » ) il faut
transformer l’égalité jusqu’à ce « x = ………..» solution
1 : on pose par le
produit en croix , on écrit :
1 fois x = 2 fois 18
soit x = 36
vérification :
On se pose la question : est ce
que ainsi combien fait : Conclusion : x = 36
est solution de l’équation |
|
|
Le tiers d’un
nombre est de 9 . Quelle est la valeur
de ce nombre ? |
|
|
Le cinquième d’un nombre
plus 5 est égal à 20 . Quelle est la
valeur de ce nombre ? |
|
|
Le double d’un nombre
- 5 est égal à 20 Quelle est la valeur de ce nombre ? |
|
|
Les ¾ d ’ un nombre égal
15 . Quel est ce nombre ? |
|
|
Un nombre plus le double
de ce nombre vaut 18 . Quel est ce nombre ? |
|
|
le nombre + 1/3 du nombre = 24 . Quel est ce
nombre ? |
|
|
1/3 du nombre + 2/5
du nombre = 44 . Quel est ce nombre ? |
|
|
¾ du nombre + 1/3 du
nombre = 26. Quel est ce
nombre ? |
|
|
¼ du nombre + 20 = 36
. Quel est ce nombre ? |
|
|
3/5 du nombre -15 =
21. Quel est ce nombre ? |
|
|
Les ¾ des 5/7 d ’ un
nombre valent 45. Quel est ce nombre ? |
|
|
8) Trouver un nombre qui , augmenté de son 1/3
, égale 24 ; égale 36 ; égale 80 ; égale
120.(indications :x + 1/3 x =24 =donc 4/3 du nombre =24) |
|
Problèmes (ces problèmes sont traités dans le cours n°11
niveau V )
Méthode :il faut ;…
1.
Identifier l’inconnue . 2. Ecrire
une équation . 3. Résoudre l’équation.
4. Conclure .
N°3: : Un rectangle a les
caractéristiques suivantes : Son
périmètre mesure 80 m ; sa longueur est le triple de sa
largeur .
Calculer sa longueur et sa largeur .
N°4 : Trouver 3 nombres entiers pairs consécutifs dont
la somme est égale à 36 . Donner la valeur du premier nombre.
N°5 : Une ouvrier met 15 minutes pour usiner une pièce , pour aménager et préparer le
poste de travail il faut prévoir 3h 45 mn. Combien de pièces peut-il
usiner sur une semaine de 35 heures ?
Prendre "x"
le nombre de pièces..( transformer la
durée en nombre décimal)
N°10 Quel nombre
faut-il multiplier 34 pour obtenir 25 ?
SUITE
: Interdisciplinarité :
N°1 Le réservoir d'une voiture est au deux cinquièmes rempli.
Il faut ajouter 38 litres de
carburant pour le remplir entièrement . Quelle est la contenance de ce
réservoir ?
N°3 la largeur d'un
rectangle est le tiers de sa longueur et
le périmètre mesure 48 m . Calculer les dimensions de ce rectangle .
N°4 La longueur d'un
rectangle surpasse de 10 m sa largeur .
Le périmètre est de 120 m .Calculer les dimensions de ce rectangle .
N°7 Calculer le pourcentage
d'augmentation de la population d'un village qui passe de 3764 habitants à 3978
.
N°8 Un
centre de formation organise un voyage .Le transporteur propose un prix global
correspondant à 160 € par personne . Si le nombre de personnes
augmente de 5 , on passe pour le même prix
global , à 120 € par personne.
Combien de personnes
participent au voyage ?
N°12
|
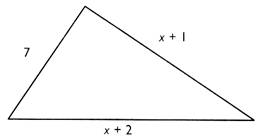
Un triangle a les
dimensions ( en m) indiquées sur la figure . Exprimer le périmètre
du triangle en fonction de "x". Calculer
"x" pour que le périmètre
soit égal à 30 m . En déduire les dimensions du triangle . |
|