|
Leçon |
TRAVAUX d ’
AUTO - FORMATION sur |
|
N°11 |
RESOUDRE UNE EQUATION du premier degré à 1 inconnue et PROBLEMES DU PREMIER DEGRE |
( vous
devez vous aider du cours !!!!!)
|
|
a) Donner la définition
d ’ une « équation »
b) Donner la définition
d ’ une « équation du
premier degré »
c) Donner la définition
d ’ une « équation du
premier degré à une inconnue »:
d) Que signifie : « Résoudre une équation »
2°)
Définition « membre ; terme ; facteur » .
Compléter les phrases suivantes : ( mots :
gauche ;deuxième membre ; plusieurs facteurs ; premier
membre ; produit de facteurs ;
les deux membres ; nombre ; droite ; ´ ; lettre )
a) Dans une égalité l’expression algébrique à gauche du
signe « égal » est appelé « ……………….….. »
b) Dans une égalité l’expression algébrique à droite du signe « égal » est appelé
« …………………… » .
c) Dans une
équation , le signe " =
" sépare les …………………
a)
Terme : un terme est composé
de un ou ………………….. .
e) Facteur : un facteur est un ………….
ou une ………………….situé à …………………et à ………….du signe
( on dit qu’un terme est constitué d’un …………………… )
3°) Que signifie "résoudre" une équation
du premier degré à une inconnue ?
4 °)
Compléter les phrases suivantes :
a)
L'équation du type a x = b :
Avec les mots à placer : solution unique x = ![]() ;
décimaux ; 0 ; on divise
;
décimaux ; 0 ; on divise
- L'équation du
type a x = b ( "a" et "b" sont des
nombres …………….. et "a" ¹ ……..)
admet une ……………………………
- Cette solution est
obtenue par une seule opération : ………………. les deux membres de l'égalité par le même
nombre "a" .
b )L'équation du type
a x+ b = c
les mots à placer: 0; décimaux ;
unique ; divise ;deux ; l'opposé de "b" ; a ;de
membre il change de signe ;
- L’équation du type
a x+ b = c ( « a » ,
« b » et « c » sont
des nombres ……………… et « a » ¹ ……) admet une solution ………….
)
- Cette solution est
obtenue par …………. opérations :
- On ajoute aux deux
membres ……………. . On dit que : si
« b » change ………………………………………….
- On ……. les deux
membres de l'égalité par le même nombre "……"
.
5°) Donner
la procédure permettant de résoudre un problème du premier degré.
|
™ |
1°) Entourer l’équation les
premiers degrés :
x ²+ 3 =
0 ; x + 3 = 0 ; 2y²
+ 5 = 0 ; 2x + - y - 4z =
15 ; x y = 6z ; x - y = 6z ; 2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
![]() x
+ y = 18 ;
x
+ y = 18 ;
2°) Entourer les équations
du premier degré à une inconnue
.
x ²+ 3 = 0 ; x
+ 3 = 0 ; 2y² + 5 = 0 ; 2x + - y - 4z = 15 ; x y = 6z ; x - y = 6z ;
2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
x² y = 6z ;
3°) Dans les égalités suivantes entourer le premier
membre :
x - y = 6z ; x + 3 = 0
4°) Dans les égalités suivantes entourer le second membre .
2y² + 5 = 0 ; 2x
+ - y = - 4z +
15
5°)
a) Entourer les
différents termes en
« x » .( il faudrait
savoir : transformer les expressions
en sommes algébriques )
x + 3 = 0 ;
2x - 8 =
- 4x + 15 ; - 3
x +15 + x = 2 x
+ 7
b) dans les égalités suivantes citer les termes des
égalités.
1x + 3 = 0 ;
2x - 8 =
- 4x + 15 ; - 3
x +15 + x = 2 x
+ 7
6°) Résoudre les exercices
suivants : (le
corrigé est dans le cours)
|
N° |
Exercices |
Résultat : |
note |
|
1 |
1 x = 7 |
|
|
|
2 |
5 x = 45 |
|
|
|
3 |
5+ x = 45 |
|
|
|
4 |
5 - x = 45 |
|
|
|
5 |
x -5 = 45 |
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
Exercices
(suite)
Résoudre les équations
suivantes ( l'inconnue est la lettre , si nécessaire , arrondir le
résultat à 0,01 près .)
Série :1
|
|
Exercices |
Résultat |
note |
|
1 |
6x = 54 |
|
|
|
2 |
2x = 6,5 |
|
|
|
3 |
7x = 84 |
|
|
Série : 2
|
|
Exercices |
Résultat |
note |
|
1 |
1,1x = - 143 |
|
|
|
2 |
4 x = 2,4 |
|
|
|
3 |
3x = 3,71 |
|
|
Série : 3
|
|
Exercices |
Résultat |
note |
|
1 |
24 z = - 9,6 |
|
|
|
2 |
3 z = 26,1 |
|
|
|
3 |
7,1 z = 435,2 |
|
|
Série : 4
|
|
Exercices |
Résultat |
note |
|
1 |
X+ 3 = 7 |
|
|
|
2 |
X + 13 = 21 |
|
|
|
3 |
X + 18 = 6 |
|
|
Série : 5
|
|
Exercices |
Résultat |
note |
|
1 |
X+ 23 = 0 |
|
|
|
2 |
X - 11 = 0 |
|
|
|
3 |
X + 2,13 = 0,3 |
|
|
Série : 6
|
|
Exercices |
Résultat |
note |
|
1 |
-x + 7 = 2 |
|
|
|
2 |
- x + 3 = 5 |
|
|
|
3 |
-2 - x = 6 |
|
|
Série : 7
|
|
Exercices |
Résultat |
note |
|
1 |
3x + 15 = 25 |
|
|
|
2 |
2x + 6 = 13 |
|
|
|
3 |
7x + 67 = 89 |
|
|
Série : 8
|
|
Exercices |
Résultat |
note |
|
1 |
5y - 3 = 7 |
|
|
|
2 |
2y + 3 = 1 |
|
|
|
3 |
12 y - 62= 14 |
|
|
Série : 9
|
|
Exercices |
Résultat |
note |
|
1 |
4x - 32 = 0 |
|
|
|
2 |
2 x +2,4 = 0 |
|
|
|
3 |
0,3 x - 2,1 = 0 |
|
|
Série : 10
|
|
Exercices |
Résultat |
note |
|
1 |
6x - 5 = 4 |
|
|
|
2 |
0,3 x + 1 = 1,9 |
|
|
|
3 |
5x - 5 = - 32 |
|
|
Série : 11
|
|
Exercices |
Résultat |
note |
|
1 |
- 1,3 x + 4,1 = 0 |
|
|
|
2 |
- 17,4 x + 53,2 = 3,1 |
|
|
|
3 |
0,4 x - 1,2 = 0 |
|
|
Série : 12
|
|
Exercices |
Résultat |
note |
|
1 |
|
|
|
|
2 |
|
|
|
Série : 13
|
|
Exercices |
Résultat |
note |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
Série : 14
|
|
Exercices |
Résultat |
note |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
EXERCICES et PROBLEMES : Mettre en équation et
résoudre. (on pose « x » l’inconnue) |
|
|
Les ¾ d ’ un nombre égal 15 .Quel est ce nombre ? |
|
|
le nombre + 1/3 du
nombre = 24 . Quel est ce nombre ? |
|
|
1/3 du nombre + 2/5 du nombre = 44 . Quel est ce
nombre ? |
|
|
¾ du nombre + 1/3 du nombre = 26. Quel est ce
nombre ? |
|
|
¼ du nombre + 20 = 36 . Quel est ce nombre ? |
|
|
3/5 du nombre -15 = 21. Quel est ce nombre ? |
|
|
Les ¾ des 5/7 d ’ un nombre valent 45. Quel est ce
nombre ? |
|
|
Trouver un nombre qui , augmenté de son 1/3 , égale
24 ; égale 36 ; égale 80 ; égale 120.(indications :x +
1/3 x =24 =donc 4/3 du nombre =24) |
|
Problèmes
(ces problèmes sont
traités dans le cours)
Enoncé 1 :
On achète 3 kilogrammes de fruit
à 37,50 F. Quel est le prix d' un
kilogramme de fruit ?
On demande :
1.
Identifier l’inconnue .
2.
Ecrire une équation .
3.
Résoudre l’équation.
4.
Conclure .
Enoncé N°2
On achète 3 kilogrammes de fruit , je donne un
billet de 5 € , la caissière me rend 0,2 € .Quel est le prix d' un
kilogramme de fruit ?
On demande :
1.
Identifier l’inconnue .
2.
Ecrire une équation .
3.
Résoudre l’équation.
4.
Conclure .
N°3: : Un rectangle a les
caractéristiques suivantes :
Son périmètre
mesure 80 m ; sa longueur est le
triple de sa largeur .
Calculer sa longueur
et sa largeur .
N°4 : Trouver 3 nombres entiers pairs consécutifs dont
la somme est égale à 36 . Donner la valeur du premier nombre.
N°5 : Une ouvrier met 15 minutes pour usiner une pièce , pour aménager et préparer le
poste de travail il faut prévoir 3h 45 mn. Combien de pièces peut-il
usiner sur une semaine de 35 heures ?
Prendre "x" le nombre de pièces..( transformer la durée en nombre
décimal)
N°6 : trouver trois nombres entiers consécutifs dont la
somme est 1884 .( prendre pour inconnue , le plus petit nombre.)
N°7 : Trouver
3 nombres multiples de 3 consécutifs dont la somme est 27
Prendre pour inconnue le plus petit nombre .
N°8 : Trouver 5 nombres entiers impairs consécutifs dont
la somme est 75.
Info : prendre pour
inconnue le nombre médian ( celui qui se trouve au milieu )
N°9 :Trouver 13
nombres consécutifs dont la somme est 2457 .
Info : prendre pour inconnue
le nombre médian ( celui qui se trouve au milieu )
N°10 Quel nombre
faut-il multiplier 34 pour obtenir 25 ?
SUITE :
Interdisciplinarité :
N°1 Le réservoir
d'une voiture est au deux
cinquièmes rempli. Il faut ajouter 38
litres de carburant pour le remplir
entièrement . Quelle est la contenance de ce réservoir ?
N°2 Le
réservoir d'un voiture est vide aux deux
tiers . On ajoute 30 litres de carburant pour le remplir aux trois quarts . Quelle est la contenance
du réservoir ?
N°3 la largeur d'un rectangle est le tiers de sa longueur et le périmètre
mesure 48 m . Calculer les dimensions de ce rectangle . ( 6 et 18 m)
N°4 La longueur d'un rectangle surpasse de 10 m sa largeur . Le périmètre est de 120 m
.Calculer les dimensions de ce rectangle . ( 25 et 35 m)
N°5 Le 1er janvier 1997 la population de la France
a été estimée à 58 494 000 habitants
se répartissent en 30 017 000
femmes et 28 477 000 hommes.
Quel pourcentage de la population les femmes et les hommes représentent
- ils ?
N°6 Augmenter un
nombre de x % , c'est multiplier ce nombre par
( 1 + ![]() )
ou ( 1 + 0,01x )
)
ou ( 1 + 0,01x )
Pour calculer le
pourcentage d'augmentation du prix d'un
objet qui passe de 34 à 39,5 € , on
écrit : 39,5 = 34 ( 1 + 0,01 x)
Ecrire cette équation sous la forme ax + b = c , puis la résoudre ( arrondir à 0,01
près , ou à 2 décimales).
Enoncer le résultat sous forme d'une phrase .
N°7 Calculer le pourcentage d'augmentation de la population
d'un village qui passe de 3764 habitants à 3978 .
N°8 un centre de
formation organise un voyage .Le transporteur propose un prix global
correspondant à 160 € par personne . Si le nombre de personnes
augmente de 5 , on passe pour le même prix
global , à 120 € par personne.
Combien de personnes participent au voyage ?
N° 9 La durée de
fabrication d'une pièce est de 6,50 mn.
Au cours d'une journée de 8 h , combien peut-on fabriquer de
pièces sachant qu'il faut compter 1 h 30 mn pour le réglage la machine et
l'affûtage de l'outil et l'approvisionnement .
N° 10
|
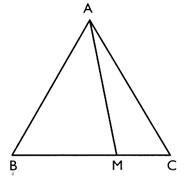
ABC est un triangle équilatéral de côté 6 cm On place sur le côté [BC] le point M tel que BM = d. 1°) calculer la hauteur du triangle ABC , puis l'aire du
triangle . 2) où doit -on placer le point M pour que l'aire du
triangle AMC soit égal à 10? |
|
N°11 .
|
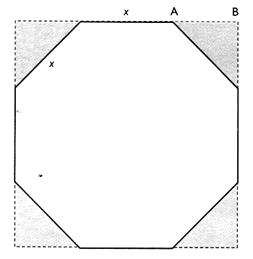
On veut découper dans une plaque carrée de 0 cm de côté un
octogone régulier de côté "x". a) Sachant que chaque triangle hachuré est un triangle rectangle isocèle ,
déterminé la mesure de chacun de leurs angles aigus . b) Calculer la longueur AB en
fonction de "x" , puis la longueur "x". |
|
N°12
|
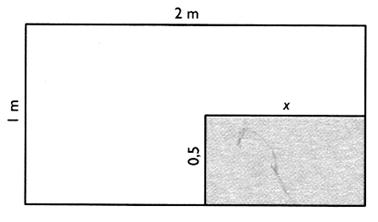
Dans une pièce rectangulaire de 2 m de longueur et de 1 m de
large , on effectue une découpe de forme rectangulaire comme l'indique la
figure ci -dessous. Donner l'expression de l'aire de la partie restante en
fonction de "x". Calculer "x" pour que l'aire de la partie
restante soit 1,25 m² . |
|
|
N°13
|
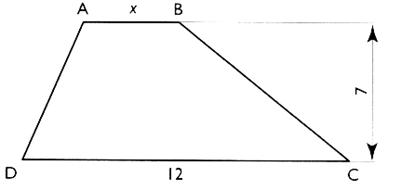
On considère un trapèze ABCD. Vérifier que l'aire du trapèze peut s'écrire :A = 8,5 x Calculer "x" pour que l'aire du trapèze soit
égale à 172,2 cm² ( arrondie à deux décimales) |
|
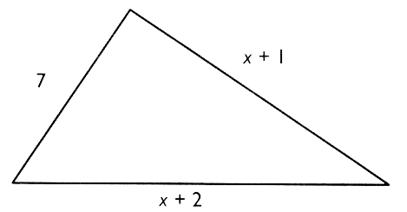
N° 14
|
Un triangle a les dimensions ( en m) indiquées sur la figure
. Exprimer le périmètre du triangle en fonction de
"x". Calculer "x" pour que le périmètre soit égal à 30 m . En déduire les
dimensions du triangle . |
|
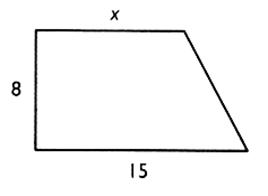
N°15
|
Montrer que l'expression de l'aire du trapèze rectangle en fonction
de "x" est : A = 4 x + 60 Calculer "x" pour que l'aire du trapèze
rectangle soit égale à 200 cm² . Pour cela , résoudre l'équation : 4x + 60 =
200 |
|