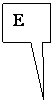|
CORRIGE |
|
|
N°8 |
TRAVAUX d ’ AUTO - FORMATION sur LES TABLEAUX NUMERIQUES et le REPERAGE sur une droite et dans un plan |
TRAVAUX CORRIGE N°8 d ’ AUTO -
FORMATION : EVALUATION:
Exercice N°1
Les 78 apprentis d'un
centre de formation se répartissent
suivant le tableau suivant:
|
Ebéniste |
24 |
|
Sculpteur |
23 |
|
Tapissier |
12 |
|
Agenceurs |
10 |
|
Restaurateur |
9 |
|
Total |
78 |
Compléter le tableau . Traduire par une phrase la 2ème ligne
du tableau .
N°2.
Un magasin de sport propose
des vêtements en trois tailles dans deux
couleurs différentes .La répartition du stock est :
-
en jaune : S (petit) : 7 , M (moyen)
12 ; L (large) 10
-
en vert : il possède un total 45
vêtements dont 8 S (petit)
et 25 L (large) soit au total : 45
Compléter le tableau et traduire par des phrases les cases
notées par " * "
|
|
S |
M |
L |
total |
|
Jaune |
7 |
12 |
10 |
*29 |
|
Vert |
8 |
*12 ( 45 )- (12+8) |
25 |
45 |
|
Total |
*15 ; ( 8+7) |
24 ; ( 12+12
) |
35
( 10+25) |
74
( 45+29) |
3°) Compléter ce tableau .
|
|
Garçons |
Filles |
Total |
|
Cinéma |
8 |
c) 4 |
12 |
|
Sport |
e) 4 |
d) 5 |
b) 9 |
|
Lecture |
6 |
1 |
a) 7 |
|
TOTAL |
f) 18 |
10 |
28 |
a)Combien d’élèves ont pour loisir favori le cinéma ? 12
b)Parmi les garçons combien ont pour loisir favori le
cinéma ? 8
B )
Repérage sur une droite
Exercice :
Sur un axe ( x' x ) on définit un repère ( O,I ) d
'unité 1 cm .Placer sur cet axe les
points A , B , C , M , N , P d'abscisses respectives : -3 ;2,5 ;2,8 ; 4 ; -4,2
; 5,3 .
|
|
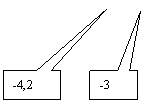
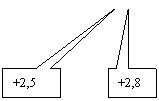
Pour chaque exercice : objectif : savoir Graduer une droite et donner
des abscisses.
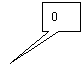a)
Déterminer la longueur unité "u" ; placer le point origine ; donner les abscisses entières comprises
entre les deux points représentés.
|
|
7 cm = 1,5 - ( -5,5)
= 7 u donc u= 1 cm
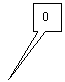b) Déterminer
la longueur unité "u" ; placer le point origine ; donner les abscisses entières comprises
entre les deux points représentés.
|
|
Soit 10 cm pour 5 graduations ( calcul : 3 - ( -2)
= 5 ) donc 1 unité = 10 cm :5
= 2 cm
d )
Déterminer la longueur unité "u"
; placer le point origine ;
donner les abscisses entières comprises entre les deux points représentés.
|
|
Soit 4 cm pour 4 graduations ( calcul 5 - (+1) =
4 ) ; soit 1 graduation = 1
cm .
C ) Repérage dans un plan .
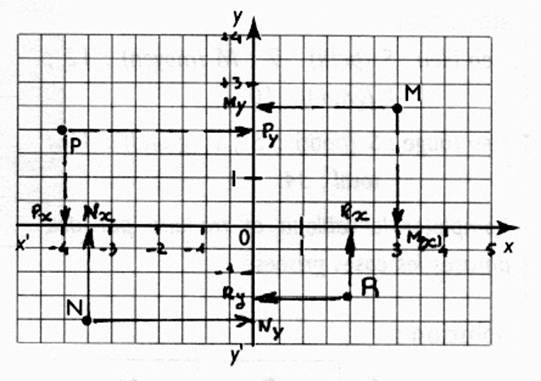
1°) A partir du dessin ci dessous ,compéter le tableau:
|
|
Coordonnées des points :
|
|
Abscisse |
Ordonnée |
Coordonnées |
|
|
M |
+3 |
+2,5 |
( +3 ; +2,5 ) |
|
|
P |
-4 |
+2 |
( -4 ;+2 ) |
|
|
N |
-3,5 |
-2 |
( -3,5 ; -2 ) |
|
|
R |
+2 |
-1,5 |
( +2 ; -1,5 ) |
|
N°2 :Sur une feuille
quadrillée , dessiner un repère du plan ( cartésien et deux axes perpendiculaires ) d'unités 1 cm
sur chaque axe .
Placer les points
: A ( 1 ; 1 ) ; B ( 3 ,- 5) ; C ( -1 ; 1 ) ; D ( 0;0 ) ; E ( - 4,6 ; 2,8
)
|
|
SERIE 1 Repérage : représentation graphique d’une FONCTION.
1°) :
Représenter une fonction dans un repère.
Compléter la phrase suivante :
La représentation
graphique d’une fonction f dans un repère est constituée par tous les points dont les coordonnées sont ( x ; y
) ou , puisque y = f(x) ; (
x ; f(x))
2 °)Représenter
graphiquement les points appartenant à la fonction dont l’équation est f1(x) = 2,5 prendre x pour des valeurs de x comprises entre 0
inclus et 4 inclus . ( notation
[ 0 ; 4 ] )
Utiliser le tableau suivant :
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
|
x |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
f1(x) |
0 |
1,25 |
2,5 |
3,75 |
5 |
6,25 |
7 ,5 |
8,75 |
10 |
Solution : représentation graphique des
points :
3°) soit f2(x) = x -
1 ; pour x [0 ; 5 ]
a) Compléter
le tableau suivant:
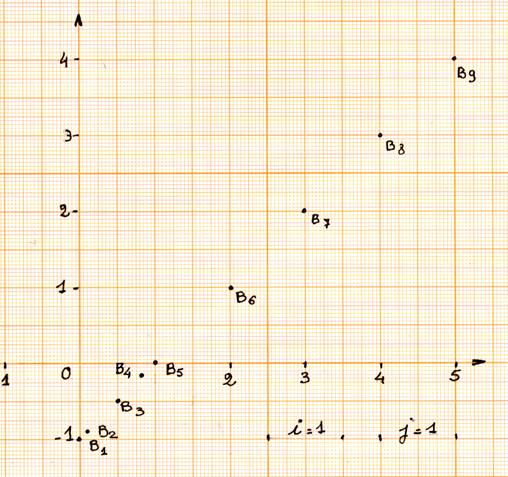
b) Placer les points Bn dans un repère cartésien .
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
B7 |
B8 |
B9 |
|
x |
0 |
0,2 |
0,5 |
0,8 |
1 |
2 |
3 |
4 |
5 |
|
f2(x) |
0 |
-0,8 |
-0,5 |
-0,2 |
0 |
1 |
2 |
3 |
4 |
4
°) soit l’équation f3(x) =
-2x + 0,5 ,
a) Compléter
le tableau suivant: [-5 ; 0 ]
b) Identifier les points avec une lettre et placer
ces points dans un repère cartésien.
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
f3(x) |
+0,5 |
0,9 |
1,5 |
2,1 |
2,5 |
4,5 |
6,5 |
8,5 |
10,5 |
Représentation graphique :
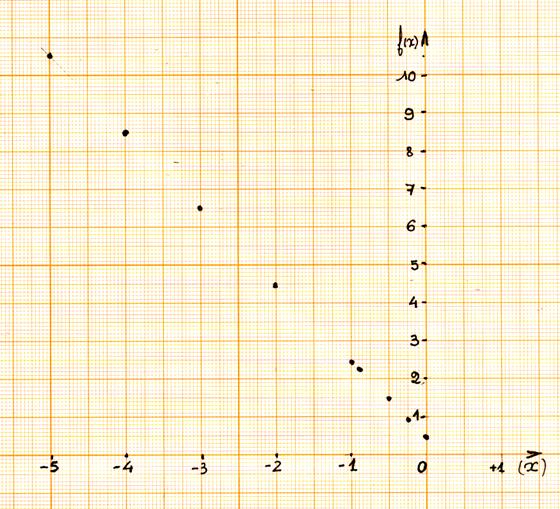
5° ) Compléter le
tableau pour f 4(x)
= ‑ 0,5x
Identifier les points avec une lettre et placer ces
points dans un repère cartésien.
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
f 4(x) |
0 |
0,1 |
0,25 |
0,4 |
0,5 |
1 |
1,5 |
2 |
2,5 |
6°) Tracé de
la fonction x² :
soit : f1
= y1 ;
telle que f1(x) = x2
I ) compléter les deux tableaux :
a) Tableau
1 :
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
x2 = y1 |
0 |
0,04 |
0,25 |
0,64 |
1 |
4 |
9 |
16 |
25 |
b) Tableau
2 :
|
x |
0 |
0,2 |
0,5 |
0,8 |
1 |
2 |
3 |
4 |
5 |
|
x2 = y 1 |
0 |
0,04 |
0,25 |
0,64 |
1 |
4 |
9 |
16 |
25 |
c) Faire
une représentation graphique de
x²
Dont la base est : i = 1cm et j = 0,5 cm
III ) soit: f2 = y2 ; telle que f2(x) = x2
a) Construire un tableau , pour les valeurs de « x » prendre de 0,1
en 0,1 .
a)
tableau :
|
x |
-1 |
|
|
|
|
|
|
|
|
-0,1 |
0 |
|
|
|
|
|
|
|
0,8 |
0,9 |
1 |
|
f2(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b)Faire une représentation graphique de f2(x)
Dans la base
i = 5cm et j =,5 cm avec
« x » [ -1 ; +1 ]
que l’on note
aussi : pour « x »
compris -1 £ x £ + l
(-1 £ x £ + l
et x = [ -1 ; +1 ] sont des écritures équivalentes )
b)
Solution I Première
représentation graphique de x² avec i = 1cm et j = 0,5 cm
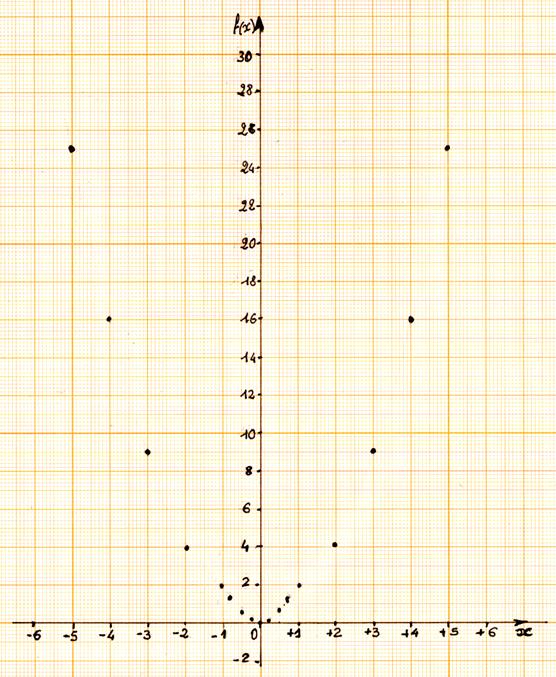
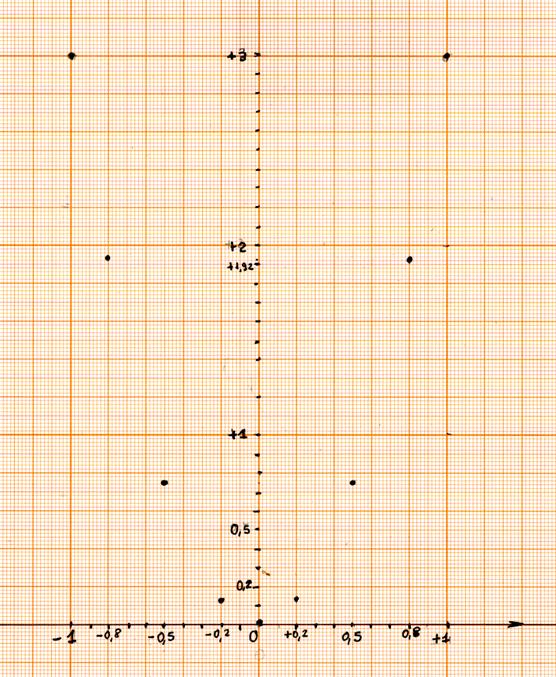
Solution II : Représentation graphique de x² ; pour
« x » compris -1
£ x £ + l, à compléter .
SERIE 2 :
Consignes :
Faire les calculs suivants ( ceux -ci ont été
déjà exécuté dans le cours
« calcul de la valeur numérique
d’une expression algébrique ).
Pour chaque tableau : sur une feuille quadrillée
, tracer un repère cartésien ,
les bornes sur « x » sont à
prendre dans le tableau . . Sur
« y » les bornes sont données par le résultat des calculs ( plus petite valeur et plus grande valeur )
1°) Compléter le tableau pour f1(x)
= 2,5 x , et placer ces points dans le repère
cartésien .
|
x |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
f1(x) |
0 |
1,25 |
2,5 |
3,75 |
5 |
6,25 |
7 ,5 |
8,75 |
10 |
2°) Compléter le tableau suivant:
f2(x) = x -
1
|
x |
0 |
0,2 |
0,5 |
0,8 |
1 |
2 |
3 |
4 |
5 |
|
f2(x) |
0 |
-0,8 |
-0,5 |
-0,2 |
0 |
1 |
2 |
3 |
4 |
3°)
soit l’équation f3(x) =
-2x + 0,5 ,
Compléter le tableau suivant:
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
f3(x) |
+0,5 |
0,9 |
1,5 |
2,1 |
2,5 |
4,5 |
6,5 |
8,5 |
10,5 |
4°) Compléter le tableau pour f 4(x) = ‑ 0,5x
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
f 4(x) |
0 |
0,1 |
0,25 |
0,4 |
0,5 |
1 |
1,5 |
2 |
2,5 |
5°) Dans le
même repère faire le tracé des fonctions
f1 = y1 ;
f2= y2 ; f3= y3 et y4
= f4, , telles que f1(x)
= x2 f2(x) = 3 x2 , f3(x) = - 2x2 et
f 4(x) = ‑0,5 x2 +1
Au préalable compléter le tableau suivant:
|
x |
0 |
-0,2 |
-0,5 |
-0,8 |
-1 |
-2 |
-3 |
-4 |
-5 |
|
f1(x) |
0 |
0,04 |
0,25 |
0,64 |
1 |
4 |
9 |
16 |
25 |
|
f2(x) |
0 |
0,12 |
0,75 |
1,92 |
3 |
12 |
27 |
48 |
75 |
|
f3(x) |
0 |
-0,8 |
-0,5 |
-1,28 |
-2 |
-8 |
-18 |
-32 |
-50 |
|
f 4(x) |
1 |
0,98 |
0,875 |
0,68 |
0,5 |
-1 |
-3,5 |
-7 |
-11,5 |
( en devoir un de ces tracés pris , au hasard ,sera à réalisé , sur
feuille )