DOSSIER : N°17: LE CERCLE et LE DISQUE

Leçon	Titre
N°17	CORRIGE : LE CERCLE et LE DISQUE

CONTROLE:

1°) donner la définition du cercle. le cercle est une ligne courbe plane , fermée, dont tous les points sont équidistants d’un point fixe appelé « centre »

2°) donner la définition du disque.

Un disque est constitué par l’ensemble des points de la circonférence du cercle et de sa région intérieur

3°) donner la définition du diamètre. Le diamètre "D" :

Le diamètre est une corde qui passe par le centre , sa mesure est le double de celle d’un rayon .

4°) donner la définition du rayon. Le rayon : Le rayon est le segment de droit qui joint le centre à un point quelconque du cercle .

5°) Donner la formule qui permet de calculer la circonférence d'un cercle. ( en fonction du rayon et en fonction du diamètre ) :

f ( diamètre) C = D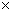p

ou f ( rayon) C = 2pr 

6°) Donner la formule qui permet de calculer l' aire du disque . ( en fonction du rayon et en fonction du diamètre ) en f ( diamètre) A =  ; f ( rayon) A = p R²

EVALUATION:

A) Tracer un cercle :

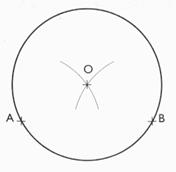
1°) Tracer un cercle de rayon 2,5 cm passant par les deux points A et B .

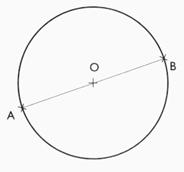
2°) Tracer un cercle de rayon 2,5 cm passant par deux points A et B distant de 4 cm .

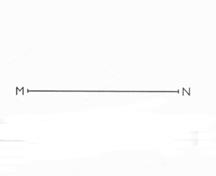
3°) Tracer un cercle de diamètre [MN] donné .

B) Calculs : ( prendre p = 3,14 )

Périmètre :

1°) Calculer la circonférence du cercle de rayon 7 cm .

C = 23,14 7 = 43,96 cm

2°) Calculer la circonférence du cercle de diamètre 7 cm .

C = 143,14 = 43,96 cm

Aire :

3°) Calculer l' aire du disque de rayon 7 cm .

Solution : ( prendre p = 3,14 )

A = p R² ;

A = p 7² ;

A = 3,14 (7 cm )² ;

A = 3,14 49 cm² = 153,86 cm²

Aire du disque de rayon 7 cm = 153,86 cm²

4°) Calculer l' aire du disque de diamètre 7 cm .

A = = =153,86 cm²

INTERDISCIPLINARITE :

LE CERCLE : LONGUEUR ET CALCUL D’ UNE DIMENSION

1) Les rayons d’une bicyclette mesurent 27 cm. Quel est le périmètre de chacune des roues ?

Périmètre = 2 fois 27 fois 3,14 = 169,56 cm

2) On veut entourer de grillage un puits circulaire de 1,15 m de rayon. Quelle longueur de grillage faudra-t-il acheter ?

Périmètre = 2 fois 1,15 fois 3,14 = 2,30 m fois 3,14 = 7,222 m

3) Une roue de bicyclette a 55 cm de diamètre. Calculer son périmètre. Quelle distance aura été parcourue après 100 tours, puis 500 tours de roue ?

Périmètre = 55 fois 3,14 = 172,7 cm

Distance pour 100 tours : 100 fois 172,5cm = 17250cm (172,50 m)

Distance pour 500 tours : 500 fois 172,5cm = 86 250 cm = (

4) Un panneau de signalisation routière a 27,5 cm de rayon. Calculer son périmètre (en mètre).

Périmètre = 2 fois 27,5 cm fois 3,14 = 172,7 cm

P = 1,727 m

5) On remplace le galon sur les deux cercles d’un abat-jour. Quelle sera la longueur de galon nécessaire si les diamètres des deux cercles sont respectivement de 30 cm et 35 cm ?

P₁ = 30 fois 3,14 = 94,2 cm

P₂ = 35 fois 3,14 = 109,9 cm

Total de galon : 94,2 + 109,9 = 204,1 cm

6) Calculer le périmètre du cercle ci-dessous.

25 m

P= 3,14 fois 25 = 78,5 m

7) Ma bicyclette a des roues de 700 mm de diamètre. Calculer la distance effectuée lorsqu’elles font trois tours.

Distance pour trois tours : 3,14 fois 700 fois 3 = 6594 mm ( 6,594 m)

8) Une fillette joue avec un cerceau de 80 cm de diamètre. Combien de tours complets le cerceau a-t-il effectué si elle l’a lancé sur une distance de 21 m ?

Distance parcourue pour 1 tour : 3,14 fois 80 = 251 ,2 cm = 2,512 m

Nombre tours : 21m : 2,512m = 8,35

Conclusion le cerceau fera 8 tours complets.

9) Sur une plaque de liège, François confectionne une cible pour jouer aux fléchettes. Avec du ruban adhésif de couleur, il veut représenter cinq cercle ayant pour rayon respectif : 4 cm, 8 cm, 12 cm, 16 cm et 20 cm. Il dispose de deux rubans adhésifs de 3 m chacun. Quelle longueur de ruban lui restera-t-il (au cm près) ?

10) Un arbre a une circonférence de 3,768 m. Calculer son diamètre.

11) Un disque 33 tours tourne 33 fois sur lui-même en une minute. Son diamètre étant de 30 cm, calculer la distance parcourue par un point quelconque du périmètre si la face dure 15 mn, puis 20 mn 45 s.

AIRE DU DISQUE

Une table de salon circulaire a un rayon de 32 cm. Quelle est son aire ?

12) On veut couvrir un puits circulaire de 55 cm de rayon avec une plaque métallique qui devra dépasser le bord du puits de 5 cm. Quelle sera l’aire de cette plaque ?

13) Pour décorer une petite table ronde de 50 cm de diamètre, maman confectionne un napperon d’un diamètre inférieur de 15 cm à celui de la table. Quelle est l’aire du napperon ?

14) Une pelouse circulaire a 47,10 m de périmètre. Calculer son aire.

15) Sur le mur d’un collège, un artisan réalise une mosaïque circulaire de 6 m de diamètre. Il est payé 329 F par m² posé. A combien revient la pose de cette mosaïque ?

16) Pour confectionner un dessous-de-plat, papa découpe, dans une planche carrée de 22 cm de côté, un disque qui touche les 4 côtés de la planche. Quelle est l’aire du dessous-de-plat ? Quelle est l’aire de planche inutilisée ?

17) Un disque de 33 tours a un diamètre de 30 cm. Le trou central a 7 mm de diamètre. Calculer l’aire de la surface pleine (au mm² près).

18) Un massif de fleurs a la forme d’un disque de 6,50 m de diamètre. Le jardinier doit y planter des rosiers et il estime qu’il faut environ 0,15 m² pour chaque plant. Combien de rosiers faudra-t-il prévoir ?

19) Un couple a racheté un vieux moulin et entreprend sa restauration. Le moulin, de forme cylindrique, mesure 6,4 m de diamètre intérieur et comprend deux pièces superposées. Pour repeindre les plafonds avec deux couches de peinture, combien de pots de 2,5 l seront nécessaires si un pot couvre 35 m² ?

20) Une table ronde de 1,10 m de diamètre est utilisée pour un repas de famille. On lui ajoute, au milieu, deux rallonges rectangulaires mesurant chacune 0,40 m sur 1,10 m. Quelle est l’aire totale obtenue ?

21) 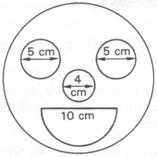Un enfant a réalisé en peinture un dessin représenté par la figure ci-dessous. Le visage, d’un diamètre de 20 cm, est peint en rose, le nez et la bouche en rouge ; les yeux sont laissés blancs. Calculer les aires des surfaces roses, rouges et blanches.