LECON N°11 CORRIGE	Devoir : Ÿ Remédiation : Ÿ	Nom :…………	Classe : Groupe :
Date :……………	Rattrapage : Ÿ Soutien : Ÿ	Prénom :…………	Note contrôle :	Note évaluation :

:

DEVOIR n°2 ; leçon N°11 sur Résoudre une équation du premier degré et PROBLEMES DU PREMIER DEGRE

Corrigé

EVALUATION: CORRIGE

1°) Série d ’ exercices

Résoudre les équations suivantes si nécessaire , arrondir le résultat à 0,01 près .)

	Exercices	Résultat	note
1	2x = 6,5	X = 3,25
2	1,1x = - 143	X = - 143 / 1,1 ; x = - 130,00
3	7,1 z = 435,2	Z = = 61,2957 ; z = 61,30
4	x + 13 = 21	X = 8 ; x = 8,00
5	x - 11 = 0	X = 11 ; x = 11,00
6	-x + 7 = 2	X = 5 ; x = 5,00
7	2x + 6 = 13	X = 3,5 ; x = 3,50
8	5y - 3 = 7	Y = 2 ; y = 2,00
9	0,3 x - 2,1 = 0	X = 7 ; x = 7,00
10	0,3 x + 1 = 1,9	X = 3 ; x = 3,00
11	- 1,3 x + 4,1 = 0	X = 3,1538 , ;x = 3,15
13		x = 5 ; x = 5,00
14		X = 6 ; x = 6,00
		= 12 ; x = 12,00

Pour la deuxième partie du devoir faire deux ou trois problèmes : (corrigé)

Un autre problème sera donné choisi en « interdisciplinarité » .

Série II ) Pour chaque problème: On demande :d’identifier l’inconnue , d’écrire une équation et de résoudre l’équation.

N°1: : Un rectangle a les caractéristiques suivantes :

Son périmètre mesure 80 m ; sa longueur est le triple de sa largeur .

Calculer sa longueur et sa largeur .

80 = 2 ( l + L)

40 = l + L

L = 3 fois l donc 40 = l + 3l soit 4 l ;

On en déduit : soit l = 40 / 10 = 10 soit l = 10 m

Donc L = 3 fois 10 = 30 m

N°2 : Trouver 3 nombres entiers pairs consécutifs dont la somme est égale à 36 . Donner la valeur du premier nombre.

N°3 : Une ouvrier met 15 minutes pour usiner une pièce , pour aménager et préparer le poste de travail il faut prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?

Prendre "x" le nombre de pièces..( transformer la durée en nombre décimal)

N°4 Quel nombre faut-il multiplier 34 pour obtenir 25 ? 34 x = 25 ; soit x = 25/34 ; x= 0,735 à 0,001 prés

Série III ) INTERDISCIPLINARITE : ( donner un des problèmes suivants)

N°1 la largeur d'un rectangle est le tiers de sa longueur et le périmètre mesure 48 m . Calculer les dimensions de ce rectangle . ( 6 et 18 m)

N°4 La longueur d'un rectangle surpasse de 10 m sa largeur . Le périmètre est de 120 m .Calculer les dimensions de ce rectangle . ( 25 et 35 m)

N°8 un centre de formation organise un voyage .Le transporteur propose un prix global correspondant à 160 € par personne . Si le nombre de personnes augmente de 5 , on passe pour le même prix global , à 120 € par personne.

Combien de personnes participent au voyage ?

N° 2

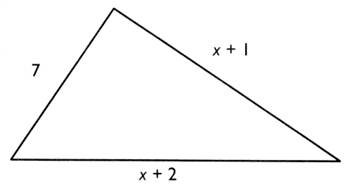
Un triangle a les dimensions ( en m) indiquées sur la figure . Exprimer le périmètre du triangle en fonction de "x". Calculer "x" pour que le périmètre soit égal à 30 m . En déduire les dimensions du triangle . 30 = 7 + x +1 + x + 2 30 = 10 + 2x 20 = 2 x x = 10 vérification : 7 + (10 +1) + ( 10 +2) = 30

N°3

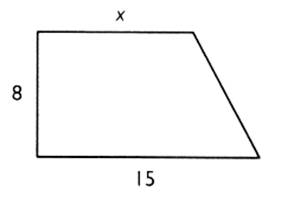
Montrer que l'expression de l'aire du trapèze rectangle en fonction de "x" est : A = 4 x + 60 Calculer "x" pour que l'aire du trapèze rectangle soit égale à 200 cm² . Pour cela , résoudre l'équation : 4x + 60 = 200

CONTROLE. CORRIGE

1°) Vocabulaire :

Donner la définition de «  Equation du premier degré . à une inconnue »:

Une équation du premier degré à une inconnue est une égalité dont un ou plusieurs termes contient une seule et même lettre est dont l’inconnue est de puissance 1 .

2°) Que signifie "résoudre" une équation du premier degré à une inconnue ?

Résoudre une équation du premier degré à une inconnue c'est rechercher après transformation et calcul une valeur de "x" qui vérifie que l'égalité numérique est "vraie".

3 °) Compléter les phrases suivantes :

a) L'équation du type a x = b :

Avec les mots : solution unique x =  ; décimaux ; 0 ;

L'équation du type a x = b ( "a" et "b" sont des nombres décimaux et "a" ¹ 0) admet une solution unique x =

b )L'équation du type a x+ b = c : Série 2 de questions : 0; décimaux ; unique ; 

e)L'équation du type a x+ b = c ( "a" , "b" et "c" sont des nombres décimaux et "a" ¹ 0) admet une solution unique )

5°) Donner la procédure permettant de résoudre un problème du premier degré .

Pour résoudre un problème , on doit respecter l'ordre de procédure suivant :

Choix de la ou des inconnues : recherche de l'inconnue : après avoir lu et analysé l'énoncé , choisir une inconnue .

a) Mise en équation : établir l' équation traduisant la situation étudiée .

b) Résolution de équation , ou d’un système d’équations du premier degré à 1 ou 2 inconnues .

c) Discussion du problème : énoncer le résultat en rédigeant une phrase et vérifier si ce résultat est conforme au problème posé .