|
Leçon |
||
|
N°11 |
DEVOIR n°1 Résoudre une équation du premier degré et
PROBLEMES DU PREMIER DEGRE |
|
|
|
||
1°)
Entourer léquation les premiers
degrés :
x ²+ 3 = 0 ; x + 3 = 0 ; 2y²
+ 5 = 0 ; 2x + - y - 4z = 15 ; x y = 6z ; x - y = 6z ; 2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
![]() x + y = 18 ;
x + y = 18 ;
2°)
Entourer les équation du premier degrés à une inconnue .
x ²+ 3 =
0 ; x +
3 = 0 ; 2y² + 5 = 0 ; 2x + - y - 4z = 15 ; x y = 6z ; x - y = 6z ; 2y + 5 = 0 ; 2x + - y - 4z² = 15 ;
x² y = 6z ;
3°) Entourer le premier membre :
x - y =
6z ; x + 3 = 0
4°)
Entourer le second membre .
2y² + 5 = 0 ; 2x + - y =
- 4z + 15
5°) Entourer les termes .( transformer les expressions en sommes
algébriques )
|
Expression : |
Somme
algébrique |
Facteurs : |
|
x + 3
= 0 |
( x ) + + 3) = 0 |
( x ) et (+ 3) |
|
2x - 8 =
- 4x + 15 |
(+2x) + (- 8 )= (- 4x) + (
+ 15) |
(+2x) ; (- 8 ) ; (- 4x) ;(+15) |
6°)
Résoudre les exercices suivants : (le
corrigé est dans le cours)
|
N° |
Exercice |
Résultat
: |
|
|
1 |
1 x
= 7 |
x = 7 |
|
|
2 |
5 x =
45 |
x = 9 |
|
|
3 |
5+ x = 45 |
x = 40 |
|
|
4 |
5 - x =
45 |
x = - 40 ( 5 =
45 + x ; x = 5 - 45 ;
) |
|
|
5 |
x -5 = 45 |
x = 50 |
|
|
6 |
|
x = 15 ;
(2 x = 3 0) |
|
|
7 |
|
x = 5/3 ;
(10 = 6 x ) |
|
|
8 |
|
x = 15 ; ( 30 = 2x ) |
|
|
9 |
|
x =5/3 ; (6 x = 10) |
|
|
10 |
|
x = 40 |
|
|
11 |
|
x = ; 5
= 2x ;
x = 2,5 |
|
Exercices (suite)
Résoudre
les équations suivantes ( l'inconnue est
la lettre , si nécessaire , arrondir le résultat à 0,01 près .)
Série :1
|
|
Exercices |
Résultat |
Note |
|
1 |
6x = 54 |
x =
9 ; ( 54 / 6 ) |
|
|
2 |
2x = 6,5 |
x = 3, 25
; ( 6,5 /2 ) |
|
|
3 |
7x = 84 |
x = 12
; ( 84 / 7 ) |
|
Série : 2
|
|
Exercices |
Résultat |
Note |
|
1 |
1,1 x = -
143 |
x = - 130
; ( 143 / 1,1 ) |
|
|
2 |
4 x = 2,4 |
x = 0, 6
; ( 2,4 / 4 ) |
|
|
3 |
3x = 3,81
|
x = 1,27
; ( 3,81 / 3 ) |
|
Série : 3
|
|
Exercices |
Résultat |
Note |
|
1 |
24 z = - 9,6 |
z = -
( 9,6 /24) = - 0,4 |
|
|
2 |
3 z =
26,1 |
z = 26,1 / 3 |
|
|
3 |
7,1 z =
435,2 |
z = 435,2 / 7,1 |
|
Série : 4
|
|
Exercices |
Résultat |
Note |
|
1 |
X+ 3 = 7 |
x = 7 - 3 ; x = 4 |
|
|
2 |
X + 13 =
21 |
x = 21 - 13 ; x = 8 |
|
|
3 |
X + 18 =
6 |
x = 6 - 18 ; x =
- 12 |
|
Série : 5
|
|
Exercices |
Résultat |
note |
|
1 |
X+ 23 = 0 |
X = - 23 |
|
|
2 |
X - 11 =
0 |
X = 11 |
|
|
3 |
X + 2,13
= 0,3 |
X = 0,3 - 2,13 ; x = 1,83 |
|
Série
: 6
|
|
Exercices |
Résultat |
note |
|
1 |
-x + 7
= 2 |
7 = x +2 ; x = 7 - 2 ; x = +5 |
|
|
2 |
- x + 3 =
5 |
- x + 3 = 5 ; + 3 = 5 + x ; 3 - 5 = x ; x = -2 |
|
|
3 |
-2 - x =
6 |
-2 - x = 6 ; -2 - 6 = x ; x = -8 |
|
Série
: 7
|
|
Exercices |
Résultat |
note |
|
1 |
3x + 15 =
25 |
3x = 25 - 15 ; 3x
= 10 ; x =
10 /3 |
|
|
2 |
2x + 6 =
13 |
2x = 13 - 6 ; 2x = 7 ; x
= 3,5 |
|
|
3 |
7x + 67 =
89 |
7 x = 89
- 67 ; 7x = 22 ; x = 22 / 7 |
|
Série : 8
|
|
Exercices |
Résultat |
note |
|
1 |
5y - 3 =
7 |
5y = 3 + 7 ; 5 y =
10 ; y = 2 |
|
|
2 |
2y + 3 =
1 |
2y = 1 -3 ;
y = -1 |
|
|
3 |
12 y -
62= 14 |
12 y = + 62 + 14 ; 12 y
= 76 ; y » 6,33 |
|
Série : 9
|
|
Exercices |
Résultat |
note |
|
1 |
4x - 32 =
0 |
4x = 32 ; x = 8 |
|
|
2 |
2 x +2,4
= 0 |
2 x = - 2,4 ; x = - 1,2
|
|
|
3 |
0,3 x -
2,1 = 0 |
0,3 x = + 2,1 ; x = 7 |
|
Série
: 10
|
|
Exercices |
Résultat |
note |
|
1 |
6x - 5 =
4 |
6x = 5 + 4 ; 6 x =
9 ; x = 9 / 6 ; x = 1,5 |
|
|
2 |
0,3 x + 1
= 1,9 |
0,3 x = - 1 + 1,9 ;
0,3 x = 0,9 ; x = 0,3 |
|
|
3 |
5x - 5 =
- 32 |
5x - 5 = - 32 ; 5 x = - 32 +5 ; 5x = -27 ; x = 5,4 |
|
Série : 11
|
|
Exercices |
Résultat |
note |
|
1 |
- 1,3 x + 4,1 = 0 |
4,1 = 1,3 x ; x » 3,15 |
|
|
2 |
- 17,4 x
+ 53,2 = 3,1 |
53,2 - 3,1 = 17,4
x ; 50,1 / 17,4 = x ; x » 2,88 |
|
|
3 |
0,4 x -
1,2 = 0 |
0,4 x = 1,2 ; x = 1,2 / 0,4 |
|
Série
: 12
|
|
Exercices |
Résultat |
note |
|
1 |
|
0,3 fois x = 21 fois 1,2 ; 0,3 x = 25,2 ; x = 84 |
|
|
2 |
|
2,5 fois 17 = 8,5 fois x ;
8,5 x = 42,5 ; x = 5 |
|
Série : 13
|
|
Exercices |
Résultat |
note |
|
1 |
|
X = 15 |
|
|
2 |
|
3x = 18 ; x = 6 |
|
|
3 |
|
|
|
Série : 14
|
|
Exercices |
Résultat |
note |
|
1 |
|
18 x = 20 ; x = 20/18 |
|
|
2 |
|
6 ( x + 4 ) = 3 fois
2 ; 6 x + 24 = 6 ; 6x =
-18 ; x = - 3 |
|
|
3 |
|
x + 3 = 24 ; x = 21 |
|
|
4 |
|
2x - 3 = 4,2 fois 5 ;
2x - 3 = 21 ; 2x =
24 ; x = 12 |
|
N°1 : Un rectangle a les
caractéristiques suivantes :
Son
périmètre mesure 80 m ; sa longueur est le triple de sa
largeur .
Calculer sa longueur et sa largeur .
nommons "x" la largeur du rectangle . l =
x
en fonction de "x" : la longueur du rectangle est L = 3x
le demi - périmètre est : L
+ l = x
+ 3x
= x ( 1 + 3) = 4 x
le périmètre est = 2 fois le
demi - périmètre : P = 2 ( 4x) = 8x
équation à résoudre : 80 = 8 x
( on divise par 8 les deux membres)
on obtient x = 10
la largeur du rectangle est de 10 m ; la longueur du rectangle est
de 3 fois 10 m soit 30 m.
vérification : P rectangle = 2 ( L + l ) = 2 ( 30 + 10 ) = 2 ( 40) = 80
N°2 :
Trouver 3 nombres entiers pairs consécutifs dont la somme est égale à 36 .
Donner la valeur du premier nombre.
on choisi "x" le premier nombre .
les deux autres nombres sont
"x + 2" et " (x+2)
+ 2 = x +4"
l'énoncer se traduit par l'équation : x + (x+2)
+ (x +4) = 36
soit x + x +x +2 + 4 =
36 ;
3x + 6 = 36
résolution de l'équation :
3x + 6 = 36 ; ( on ajoute -6 aux deux membres)
3x + 6 - 6 = 36
- 6 ;
3x = 30 ( on divise les deux membres par 3)
x = 10
conclusion : le premier nombre pair est " 10"
le deuxième nombre est 10 + 2
soit 12 ; le troisième nombre est 12 + 2 = 14
vérification : 10 + 12 + 14
est bien égal à 36 ; donc les trois nombres entiers pairs consécutifs sont 10 ; 12 ; 14 .
N°5 :
Une ouvrier met 15 minutes pour usiner
une pièce , pour aménager et préparer le poste de travail il faut
prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?
Prendre
"x" le nombre de pièces..(
transformer la durée en nombre décimal)
l'inconnue est le nombre de pièces usinées.
On met le temps sous forme décimale : 15 mn = 0, 25 h : 3h 45 = 3,
75 h; 35 h ne change pas = 35 h
Mise en équation : 0,25 x +
3,75 = 35
résolution de l'équation :
0,25 x + 3,75 = 35
0,25 x = 35 - 3,75
( un terme change de membre il change de signe )
0,25 x = 31,25 ( on divise 31,25 par 0,25 )
x =![]()
x = 125
le nombre de pièces usiner en une semaine sera de 125 pièces .
Interdisciplinarité :
N°3 la
largeur d'un rectangle est le tiers de
sa longueur et le périmètre mesure 48 m . Calculer les dimensions de ce
rectangle . ( 6 et 18 m)
N°4 La
longueur d'un rectangle surpasse de 10
m sa largeur . Le périmètre est de 120 m .Calculer les dimensions de ce
rectangle . ( 25 et 35 m)
N°8 un
centre de formation organise un voyage .Le transporteur propose un prix global
correspondant à 160 par personne . Si le nombre de personnes
augmente de 5 , on passe pour le même prix
global , à 120 par personne.
Combien de
personnes participent au voyage ?
N° 2
|
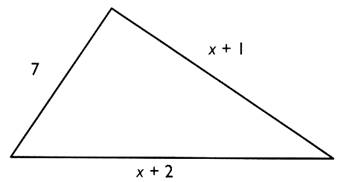
Un
triangle a les dimensions ( en m) indiquées sur la figure . Exprimer
le périmètre du triangle en fonction de "x". Calculer
"x" pour que le périmètre
soit égal à 30 m . En déduire les dimensions du triangle . |
|
Périmètre = 7 + x + 1
+ x + 2
30
= 7 + x + 1 + x + 2
30
= 10 + 2x
20
= 2x
10
= x
les
dimensions des triangle sont 7 ;
10 +1 ( = 11) ; 10+2 ( = 12)
N°15
|
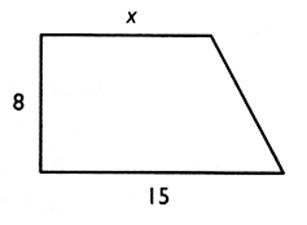
Montrer
que l'expression de l'aire du trapèze
rectangle en fonction de "x" est : A = 4 x + 60 Calculer
"x" pour que l'aire du trapèze rectangle soit égale à 200 cm² .
Pour cela , résoudre l'équation : 4x + 60 = 200 |
|
A
= ( x + 15 ) 8 / 2 = ( 8x + 120 ) /2 =
4x + 60
200
= 4x + 60 ; 140 = 4x ; x =
35