les signaux périodiques

A VENIR §§§§§§§§§§§§§§§§§§§§

Prérequis:


ENVIRONNEMENT du dossier:

Index warmaths.

Programme

Objectif suivant

tableau

DOSSIER : LES SIGNAUX PERIODIQUES

Travaux auto formatifs.

Travaux formatifs.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation


	COURS : sur : LES SIGNAUX PERIODIQUES

	Exemples de signaux périodiques : cliquez ici …..

	Qu’est ce qu’ un signal périodique ? Un signal est dit « périodique » lorsque celui-ci se reproduit identique à lui-même sur un intervalle de temps régulier. C’est par exemple le cas des battements du cœur ou le mouvement des planètes autour du Soleil.
	Qu’est-ce-que la période ? La période est la plus petite durée pendant laquelle se reproduit le phénomène identique à lui-même. C’est une grandeur qui se note T et qui peut s’exprimer en seconde, en heure ou en toute autre unité de temps. Par exemple, la période de rotation terrestre est de 24 heures ou la période d’une battement de cœur est en moyenne d’une seconde.
	Comment déterminer une période sur un graphique ? Il suffit de repérer le motif élémentaire. Il s’agit du motif qui se répète de manière régulière. On peut ensuite déterminer sa durée en tenant compte de l’échelle de représentation. Sur un graphique, l’échelle de temps se trouve toujours en abscisse. On lit donc la mesure sur cet axe. Remarque : Pour augmenter la précision de la mesure, il est nécessaire de faire la moyenne sur le plus grand nombre possible de motifs. On peut par exemple mesurer la période pour une tension sinusoïdale.
	Dans le cas d’une tension sinusoïdale, le motif élémentaire comporte une alternance positive et une alternance négative. En fait, une partie du signal est donc dans des valeurs de tension positive et la deuxième partie dans des valeurs de tension négative. C’est ce que l’on observe sur le schéma ci-dessus. Ici, le premier motif (en rouge) est compris entre t = 0 s et t = 4 s donc la période T = 4s.
	FREQUENCE :
	Qu’est-ce que la fréquence ? Par définition, la fréquence (notée 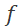) d’un phénomène périodique correspond au nombre de répétitions de ce dernier pendant une seconde. Par conséquent, plus un phénomène possède une période courte, plus il peut se répéter pendant une seconde. Il a alors une fréquence plus élevée.
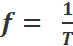
	Autrement dit : Par définition la fréquence correspond au nombre de répétions d'un phénomène périodique sur une durée d'une seconde. Pour calculer la fréquence il suffit donc de diviser une durée d'une seconde par la durée du phénomène élémentaire se qui se répète autrement dit il suffit de diviser une seconde par la période du phénomène exprimée en seconde: Avec : Avec « T » est la période en seconde. et 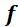est la fréquence en Hertz
	Cette relation indique que la fréquence est tout simplement l'inverse de la période
	L’unité de la fréquence L’unité légale de fréquence est le hertz de symbole Hz. Il est aussi possible d’utiliser les unités dérivées comme le millihertz, le centihertz, le decihertz.
	Quelques exemples de fréquences : – Un microprocesseur d’ordinateur de bureau fonctionne à une fréquence de l’ordre du gigahertz (un gigahertz correspond à un milliard de hertz) – Les battements de cœurs se font à une fréquence de l’ordre du hertz. – En France, le courant électrique alternatif distribué par les prises de secteur a une fréquence de 50 Hz.
	La relation entre la période et la fréquence La période T et la fréquence f sont liée par le relation : f = 1/T f en Hertz T en seconde La fréquence est donc simplement l’inverse de la période. On peut également écrire cette relation sous la forme: T = 1/F F en Hertz T en seconde Ainsi, selon que l’on souhaite calculer la fréquence ou la période on utilisera la première ou la seconde forme de cette relation





	BILAN : (résumé de cours )
	13 février 2018

	Exemples de calculs de fréquences et de périodes
	Exemple 1 : calcul d’une période La membrane d’un haut-parleur vibre à 440 Hz Donnée: f = 440 Hz Pour calculer une période on utilise la relation: T = 1/f La fréquence est exprimée dans l’unité qui convient on peut donc remplacer : T = 1/440 Donc T = 0,00227 s soit T = 2,27 ms Ou en notation scientifique T = 2,27 x 10-3 s
	Exemple 2 : calcul d’une fréquence Un courant alternatif sinusoïdal possède une période 50 ms. Donnée: T = 50 ms Pour calculer une fréquence on utilise la relation : 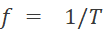Dans cette formule la période doit être exprimée en seconde, il ne faut donc pas oublier de convertir: T= 50 ms 50 : 1000 = 0,05 Donc T = 0,05 s En remplaçant la période par sa valeur on obtient: f = 1/0,05 f = 20 Hz

	Tensions maximale et minimale – La tension maximale U_max d’un signal périodique désigne la valeur la plus élevée prise par la tension u(t) au cours du temps. Elle correspond donc à l’écart entre la valeur maximale de tension et la valeur de référence. – La tension minimale U_min d’un signal périodique désigne la valeur la plus faible prise par la tension u(t) au cours du temps. Elle correspond donc à l’écart entre la valeur minimale de tension et la valeur de référence. Appareil qui permet de visualiser le signal périodique . Oscilloscope C’est avec un oscilloscope ou un système d’acquisition que l’on est capable de visualiser des signaux périodiques comme ceux observés dans les schémas précédents. Vous êtes ou serez forcément amenés à manipuler un oscilloscope lors de travaux pratiques ; il est donc intéressant de savoir comment ceux-ci fonctionnent. La nature du signal mesuré avec un oscilloscope est électrique. Les scientifiques l’utilisent généralement pour mesurer des tensions électriques. On visualise le signal sur un tube cathodique. On a donc un écran sur lequel on observe ce signal : en abscisse, le temps et en ordonnée la tension appliquée par l’utilisateur.
	HISTORIQUE :
	Origine de la découverte de la « fréquence d’un signal périodique » : Le choix du hertz comme nom de l’unité de fréquence est un hommage à Heinrich Rudolf Hertz. Ce physicien et ingénieur allemand a consacré la majeure partie de ses recherches aux ondes électromagnétiques. Il en a démontré l’existence et étudié la propagation. Ses découvertes furent le point de départ de la télégraphie sans fil, de la radiophonie et de tous les phénomènes nécessitant l’émission et la réception d’ondes électromagnétiques. Sans lui, pas de téléphones portables, pas de wifi ! Ses études sont donc d’une importance considérable. Par ailleurs les ondes radios sont aussi appelées les ondes hertziennes. Photo de Heinrich Rudolf Hertz





	Travaux auto formatifs.
	CONTROLE:



	EVALUATION:

COURS : sur : LES SIGNAUX PERIODIQUES

Exemple 1 : calcul d’une période

Exemple 2 : calcul d’une fréquence