CORRIGE
Le sujet comporte 6
pages numérotées de 1/6 à 6/6. Le formulaire est en dernière page.
La clarté des
raisonnements et la qualité de la rédaction interviendront pour une part
importante dans l’appréciation des copies.
Les candidats répondent
sur une copie à part et joignent les annexes.
L’usage de la
calculatrice est autorisé.
Exercice 1 (7,5 points)
Une entreprise assurant le service restauration à bord
des trains de voyageurs souhaite renforcer son offre. Elle effectue une étude
statistique des distances, en km, parcourues par des voyageurs en train.
L’histogramme ci-dessous présente les résultats de cette étude.

1.1.Quantitatif continue (1 point)
1.2.Compléter les colonnes, sauf la
dernière, du tableau statistique de l’annexe 1 page 5/7 à rendre avec la copie.
|
Distance parcourue en km |
Fréquence % |
Fréquence cumulé croissant % |
Effectif ni |
Centre de la classe xi |
|
|
[0 ; 200[ |
22 |
22 |
264 |
100 |
26 400 |
|
[200 ; 400[ |
40 |
62 |
480 |
300 |
144 000 |
|
[400 ; 600[ |
26 |
88 |
312 |
500 |
156 000 |
|
[600 ; 800[ |
12 |
100 |
144 |
700 |
100 800 |
|
Total |
100 |
|
1 200 |
|
427 200 |
(0,25 point par réponse juste)
1.3. =
=
1.4.Compléter le polygone des fréquences
cumulées croissantes de l’annexe 1 page 5/7 à rendre avec la copie.
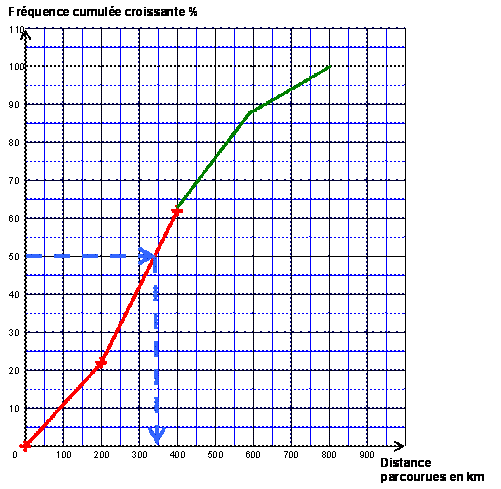
(0,5 point pour chaque point bien placé et 0,25 point pour chaque segment bien tracé)
1.5.
la valeur de la médiane dM =
Il y a autant de distance parcourues supérieures à
1.6.
La classe est [200 ;
400]. (0,5 point)
Exercice 2 (5 points)
On
considère que le prix y, en €, du billet de train est proportionnel à la
distance parcourue x en km. Le coefficient de proportionnalité qui
permet de passer de la distance parcourue au prix est égal à 0,12.
2.1. Compléter le tableau de
proportionnalité de l’annexe 2 page 6/7 à rendre avec la copie.
|
Distance parcourue en
km, x |
100 |
200 |
300 |
|
Prix du billet en €, y |
12 |
24 |
36 |
(0,5 point par
valeur juste)
2.2. Placer les trois points
de coordonnées (x ; y) dans le plan rapporté au repère de
l’annexe 2 page 6/7 à rendre avec la copie.
(0,25 point par
position juste = 0,75 point)
2.3. Les trois points de
coordonnées (x ; y) appartiennent à la représentation
graphique de la fonction f définie par f (x) = 0,12x
pour x compris entre 0 et 750.
2.3.1.
Représenter graphiquement f pour x compris entre 0 et 750 à l’aide du
repère de l’annexe 2 page 5/6. (1,25 point)
2.3.2.
Déterminer graphiquement l’abscisse du point de la représentation graphique de f
qui a pour ordonnée 42. Laisser apparent les traits utiles à la détermination.
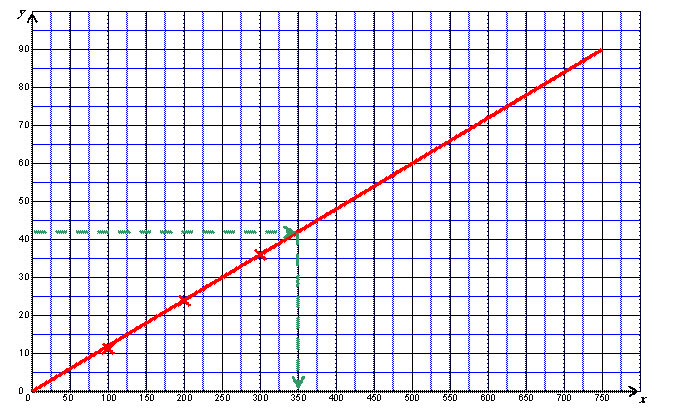
(0,5 point) pour
les traits apparents
(0,5 point) pour la
velur juste
2.4. Avec 42 €, il pourra parcourir
Exercice 3 (7,5 points)
Pour les vacances, une famille composée de 2 adultes
et de 2 enfants décide de partir à la découverte de certaines épaves de la côte
atlantique. Le centre de plongée sous-marine propose le tarif suivant :
- Pension complète : 270 € par adulte et 160 € par enfant.
- Forfait de 10 plongées encadrée : 121 € par adulte et 82 € par enfant.
- Trajet aller-retour en TGV atlantique : 156 € pour l’ensemble de la famille.
3.1.
270
2
+ 160 2
= 860 € (pensions complètes)
121
2
+ 82 2
= 406 € (Forfaits de plongée)
156
€ (tarif globale)
SOMME
= 860 + 406 + 156 = 1 422€ (1 point)
3.2. M = 1 422 =
284,40 € (1 point)
3.3.
Pour payer les 1 137,60 € restant, la famille choisit le paiement à crédit
sous la forme de 4 mensualités égales. La première est payable un mois après la
réservation du séjour. La détermination du montant x des mensualités
conduit à écrire :
4x - (1 + 2 + 3 + 4) (0,06 / 12)
x
= 1 137,6
3.3.1. 4x - (1 + 2 + 3
+ 4) ![]() x= 1 137,6
x= 1 137,6
4x - 10 ![]() x = 1 137,6
x = 1 137,6
4x - ![]() x = 1 137,6
x = 1 137,6
4x - 0,05x = 1 137,6
3,95x = 1 137,6 (2 points)
3.3.2. x = 288 Le montant de la mensualité est de 288 €. (1,5 point)
3.4.
En prévision de ce séjour la famille avait placé 560 € pendant 2 ans à intérêts
composés au taux annuel de 3,5 %.
3.4.1.
A = 560
(1 +)²
= 599,89 € (calculatrice 599,886) (1,5 point)
3.4.2.
284,4 + 288 = 572,4 Le placement permettra de payer la première mensualité. (0,5 point)