WARMATHS REPERAGE et Les Repères

• Graduation d'une droite et axe.
• Repérage sur une droite:
• Repère.
• Mesure algébrique.
• Abscisse du milieu d'un segment.
• Distance de deux points sur une droite graduée
• Repérage dans un plan.
• Coordonnées du milieu d'un segment
• Distance de deux points dans un repère orthonormal
• Quadrants

Cas particuliers

I. Graduation d'une droite et axe:

1. Graduation:

Le thermomètre est l'exemple même d'un morceau de droite graduée. Cette graduation s'appuie sur des observations physiques : degrés (Kelvin, Celsius ou Farheinheit), signification du "zéro" (température de solidification de l'eau);.. Graduer une droite c'est donc définir un "zéro" et une façon de découper cette droite. Il faut donc choisir deux points: le point d'origine de la graduation et le point unitaire tel que la distance de ce dernier au point origine soit 1, quelque soit l'unité de mesure utilisée Très souvent (mais ce n'est pas une obligation), le point origine est appelé O et le point unitaire I. Nous avons dons, dans tous les cas, OI=1. Dans le cas des graduations régulières que nous utiliserons, la droite est ensuite partagée en segments consécutifs de même longueur que [OI].

Voici différentes graduations d'une droite (D):

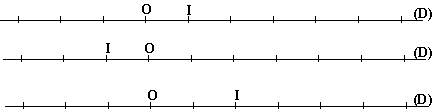
Remarque: sur la troisième graduation, le point entre O et I indique le milieu de [OI]. Ce qui entraîne que la distance entre ce milieu et O est 0,5.

2. Axe:
Un axe est une droite graduée munie d'un sens matérialisé par une flèche. Ce sens est celui de l'origine O vers le point unitaire I de la graduation. Les droites (x'x) ci dessous sont graduées de trois façons différentes. Il s'agit de trois axes :

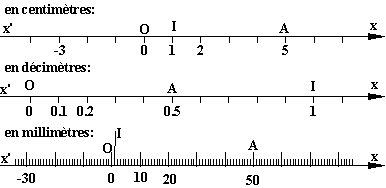
Les nombres situés sous les graduations sont les abscisses des points de graduation. Par exemples:

sur la graduation en centimètres, le point A a pour abscisse 5
sur la graduation en décimètres, le point A a pour abscisse 0.5.
sur la graduation en millimètres, le point A a pour abscisse 50.

Chaque fois le point origine O a pour abscisse 0 (zéro) et le point unitaire I a pour abscisse 1 (un).

Remarque: Le sens de O vers I est celui des nombres croissants.

II. Repérage sur une droite:

1. Repère d'une droite:

Un repère sur une droite est un axe de cette droite. Un repère est donc défini en donnant le couple de points (point origine,point unitaire)
Repérer un point sur une droite c'est définir un axe sur cette droite (=graduation et sens) et, sur cet axe, donner l'abscisse de ce point.

L'abscisse d'un point d'une droite dépend de l'axe défini sur cette droite.

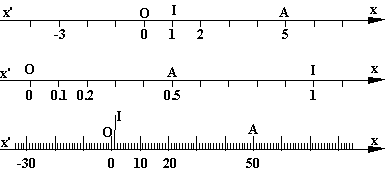
Dans les trois cas, nous avons placé le point A à 5cm du point origine O dans nos représentations. Ce qui ne signifie pas forcément que l'abscisse de A soit 5
Pour la première représentation, l'abscisse de A est effectivement 5, parce que l'unité de graduation est le centimètre. Mais pour les deux autres repères l'abscisse de A est 0,5, pour la deuxième graduée en décimètres, et.50 pour la troisième graduée en millimètres.
La distance réelle entre les points O et I ne sert que pour construire la graduation. Il est préférable, ensuite, de l'oublier et de ne considérer que la graduations réalisée.

Remarque:

Sur un axe horizontal (ou vertical) le sens choisi n'est pas toujours de la gauche vers le droite (du bas vers le haut). Les règles de lecture des abscisses restent les mêmes (valeurs croissantes dans le sens de l'axe en tenant compte de l'unité de la graduation):

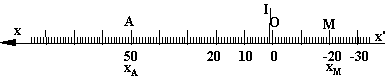
3. Mesure algébrique:
Nota: cette notion n'est pas au programme de Mathématique du collège bien qu'elle soit très facile à assimiler. Si je l'énonce c'est pour permettre une compréhension plus claire des notions de distance, de coordonnées d'un vecteur,.. et permettre des démonstrations plus générales et plus rapides. A ceux qui ne désirent pas l'étudier, il reste la faculté de mémoriser des résultats partiels basés sur la notion de distance, moins générale.

Considérons une droite (x'x) munie du repère (O,I):

Les points O, I, M, P et R ont respectivement pour abscisses 0, 1, 5, 2 et -2. Ces abscisses sont notée respectivement x_O, x_I, x_M, x_P et x_R. cette notation est très pratique lorsqu'on ne connaît pas réellement les abscisses. Avec les données ci-dessus, nous avons donc: x_O =0, x_I =1, x_M =5, x_P =2 et x_R =-2.
La mesure algébrique du segment [MP] est notée (se lit MP barre). Sa valeur est donnée par:

C'est à dire: abscisse de l'extrémité moins abscisse de l'origine du segment.
Dans notre exemple: =2-5=-3. Le nombre -3 indique que pour aller de M à P il faut parcourir 3 unités de graduation dans le sens contraire donné par l'axe.

De même: = x_P - x_R soit 2-(-2)=2+2=+4. Le nombre 4 indique que pour aller de R à P il faut parcourir 4 unités de graduation dans le sens de l'axe.

Remarque importante: les nombres et sont opposés ou encore = - puisque:

= x_P - x_R et = x_R - x_P = -( x_P - x_R ).

La mesure algébrique d'un segment d'axe est un nombre relatif entier, décimal ou réel.

La mesure algébrique n'est pas utilisée que pour un segment d'axe. Nous l'utilisons aussi dans le plan muni d'un repère (donc de deux axes). Voir plus loin.

Propriété de Chasles:

Comme = x_P - x_M et = x_R - x_P alors + = x_P - x_M + x_R - x_P = x_R - x_M
Or x_R - x_M est la mesure algébrique de [MR]. Donc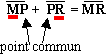
De même , d'où = x_M - x_R + x_P - x_M = 5 -(-2) +2 -5 = 4.

3. Abscisse du milieu d'un segment sur une droite graduée:

Soit (x'x) une droite graduée de repère (O,I). Les points A et B d'abscisses respectives x_A et x_B et M le milieu du segment [AB].
Comme M milieu de [AB] alors AM=MB. Le sens de A vers M est le même que celui de M vers B et comme AM et MB désigne la même distance alors les mesures algébriques de [AM] et [MB] sont égales :

Remarques:
- Nous avons remplacé la mesure algébrique de [OB] par x_B ce qui se justifie par le fait que, selon la relation de Chasles : où x_O est égale à 0 (origine du repère).
- Cette formule est juste quelque soit la position des points sur l'axe. Pour notre exemple ci-dessus : l'abscisse de M est égale à (-2 + 3)/2 = 0,5.

4. Distance de deux points sur une droite: (voir aussi Distance de deux points dans un repère du plan)
La distance de deux points M et P est la mesure absolue de la mesure algébrique du segment d'axe [MP]:

MP = ||
qui se lit : distance MP égale valeur absolue de mesure algébrique MP

Exemple : avec les données du 2°: MP=|-3|=3 et RP=|+4|=4.

La distance est donc toujours un nombre positif

Remarque:
Pour calculer MP, la procédure suivante est souvent utilisée:

- Calcul du carré de MP : MP²= ² (inutile de noter avec des | | car un carré est toujours positif comme une valeur absolue).
- Calcul de la racine carrée : MP=
- Par exemple :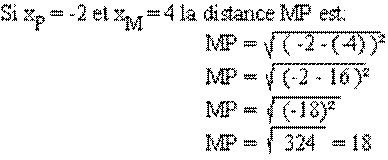
vous noterez que, dans le cas ci-dessus, nous écrivons bien ( - 18 )² et non - 18 ² (qui est égal à -324) ce qui constitue une erreur de calcul. De plus, nous ne pourrions pas alors extraire la racine carrée (la racine carrée d'un nombre négatif n'existe pas) ...

III. Repérage dans un plan:

1. Définitions:
Pour repérer un point dans un plan nous utilisons un repère composé de deux axes:
x'x pour l'axe des abscisses
y'y pour l'axes des ordonnées ( ordonnées=abscisse sur le second axe)
Ces deux axes ont le même point origine O mais des points unitaires différents I et J. On les appelle axes des coordonnées.
Remarque:
-Les deux unités de graduation ne sont pas obligatoirement égales.
- Le repère d'origine O et de points unitaires I et J est souvent noté repère(O,I,J).

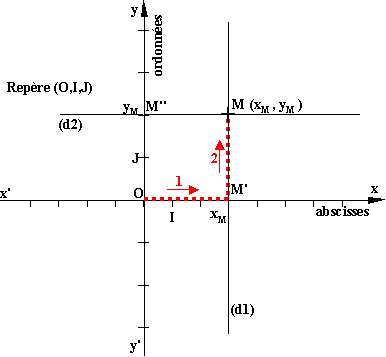
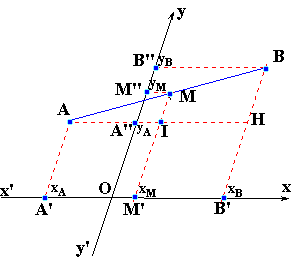
Pour repérer un point M nous avons besoin de deux nombres: une abscisse lue sur l'axe des abscisses et une ordonnée lue sur l'axe des ordonnées. Pour déterminer ces nombres nous traçons deux droites (d1) et (d2) passant par M et parallèles aux axes. Les points d'intersection M' et M" de, respectivement, (d1) et (d2) avec (x'x) et (y'y) ont pour abscisses x_M et y_M les nombres cherchés. Ces deux nombres constituent les coordonnées du point M dans le repère (O,I,J)

Attention: dans la notation M(x_M , y_M)l'ordre est important. Dans le couple (x_M , y_M) le premier nombre est toujours l'abscisse, et le second l'ordonnée. Cet ordre est illustré sur la figure ci-dessus par les flèches notée 1 et 2 pour donner le sens de la lecture des coordonnées: abscisse d'abord, ordonnée ensuite.

Exemples: d'après la figure ci-dessus nous avons M(3;2), O(0;0), I(1,0), J(0,1), M'(3;0) et M"(0;2).

2. Coordonnées du milieu d'un segment:

Soit le segment[AB] dans un repère d'axes (x'x) et (y'y). Les droites passant par A et B parallèlement aux axes, coupent (x'x) en A' et B' et (y'y) en A" et B"
A' et B' ont donc pour abscisses, les abscisses de A et de B, c'est à dire x_A et x_B. De même les ordonnées de A" et B" sont les ordonnées de A et B, c'est à dire y_A et y_B.

La droite (AA") coupe (BB') en H. Soit M le milieu de [AB]. Les droites parallèles aux axes, et passant par M, coupent (x'x) en M' et (y'y) en M". L'abscisse de M' est donc celle de M, c'est à dire xM , et l'ordonnée de M" est yM. La droite (MM') coupe la droite (AA") en I. Comme, dans le triangle ABH, la droite (MM') passe par le milieu M du côté[AB] parallèlement au côté [BH] alors (MM') coupe le troisième côté [AH] en son milieu (Théorème de la droite des milieux). I est donc le milieu de [AH]. Pour la même raison, dans les triangles AHB' et AA'B', la droite (MM') coupe [AB'] en son milieu et par suite, (MM') coupe [A'B'] en son milieu. Donc M' est le milieu de [A'B'] et son abscisse est celle de M (xM).

D'après ce que nous avons vu au II 3° , sur l'axe (x'x) comme M' est le milieu de [A'B'] alors

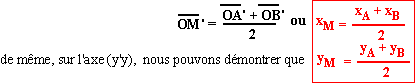
Note: pour y_M vous démontrerez que (MM") coupe [BH] en son milieu, puis vous "découperez" le parallélogramme BHA"M" en deux triangles par la diagonale [BA"]. En utilisant deux fois le théorème de la droite des milieux, vous aboutirez à : M" milieu de [B"A"] ce qui permet d'écrire: 

3. Distance de deux points dans un repère orthonormé:

Dans le repère orthonormé d'axe (x'x) et (y'y), soient les points A(x_A ; y_A) et B(x_B ; y_B).
Note préliminaire : Le choix d'un repère orthonormé est ici obligatoire pour deux raisons:
- il nous faut des axes perpendiculaires pour nous permettre d'utiliser le théorème de Pythagore (Rappel : Si MPQ est rectangle en P alors MQ²=MP²+PQ² ).
- il faut que les axes soient gradués avec la même unité pour nous permettre d'utiliser les abscisses et les ordonnées des points dans les calculs. Sinon nous ajouterions par exemple, le carré d'un nombre de centimètres, au carré d'un nombre de millimètres... Ce qui donnerait ... une très belle erreur!
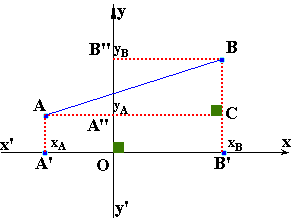
Ce qui donne la figure suivante:

Comme les lignes de rappel des abscisses (AA') et (BB') sont parallèles à (y'y) alors elles sont parallèles entre elles : (AA')//(BB') De même : comme les lignes de rappel des ordonnées (AA") et (BB") sont parallèles à (x'x) alors elles sont parallèles entre elles : (AA")//(BB"). Comme (x'x) est perpendiculaire à (y'y) alors (x'x) est perpendiculaire à toutes les droites parallèles à (y'y) et notamment à (AA') et (BB') et (y'y) est perpendiculaire à toutes les droites parallèles à (x'x) et notamment à (AA") et (BB").

Comme (BB') est parallèle à (y'y) et (y'y) perpendiculaire à (AA") alors (BB') est perpendiculaire (AA"). Appelons C le point d'intersection de (AA") et (BB').
Comme le triangle ABC possède un angle droit en C alors ABC est rectangle en C.
Comme ABC est rectangle en C alors AB²=AC²+CB². (Théorème de Pythagore).
Nous avons (voir la remarque du II 4° ) :
AC²=(x_C-x_A)² et CB²=(y_B-y_C)² d'où AB²=(x_C-x_A)²+(y_B-y_C)²
Comme les coordonnées de C sont (x_B;y_A) l'égalité ci dessus devient (en remplaçant x_C par x_B et y_C par y_A ) : AB²=(x_B-x_A)²+(y_B-y_A)² et

Exemple: avec les points A(4; -2) et B(-3;2) nous avons AB²=(-3-4)²+(2-(-2))²
AB² = (-7)²+4²=49+16 et AB²=65. En extrayant la racine carrée :
AB=

4. Quadrants:

Les deux axes de coordonnées partagent le plan en quatre parties appelées quadrants numérotés de I à IV. Les points situés dans chacun de ces quadrants présentent une organisation des coordonnées caractéristiques, comme indiquée sur la figure ci dessous

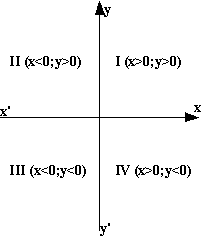
Ce qui se lit: dans le 1er quadrant (quadrant I) les deux coordonnées sont positives. Dans le quadrant II, les abscisses sont négatives et les ordonnées sont positives,etc.

5. Repères particuliers:

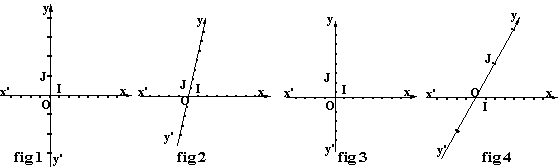
Fig 1. Repère orthogonal: les axes sont perpendiculaires. Les unités de graduation sont différentes.

Fig 2. Repère normal: les axes ont une position quelconque l'un par rapport à l'autre. Les unités de graduation sont les mêmes.

Fig 3. Repère orthonormal: c'est un repère à la fois orthogonal et normal.

Fig 4. Repère quelconque: rien de particulier ne le caractérise.

Remarque 1: Nous n'utiliserons pratiquement que des repères orthogonaux (normés ou non).
Remarque 2 : Il est parfois inutile de faire figurer l'origine et le point unitaire sur l'un ou les deux axes. Exemple : dans les centres de soins (hôpitaux, cliniques,...) un membre de l'équipe soignante relève régulièrement la température des patients. Cette température est mémorisée graphiquement sur une feuille de soin. Comme pour le patient XYZ dont la date d'admission est le 11 mai 2002.

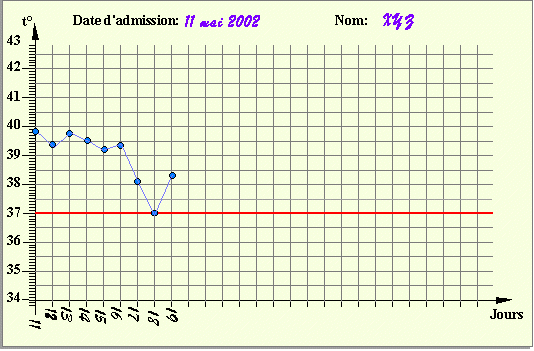
Sur ce graphique l'origine des abscisses est le 11 (qui est le 11ème jour du mois en cours) et l'origine des ordonnées est 33 (qui représente 33° de température). Chaque jour la température du patient est reportée sur le graphique : pour le patient XYZ, le jour d'admission la température était 39,8° ... le 18 elle est de 37°...
Dans ce cas, une température inférieure à 34° (hypothermie) ou une températures supérieures à 42° (hyperthermie) est généralement mortelle, d'où l'inutilité de les représenter.