Module : Géométrie .			DOSSIER : 124 – 125 – Extrait : dessins.
Warmaths  ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
LE CERCLE - LE PERIMETRE du CERCLE DESSINS
INFO COURS :
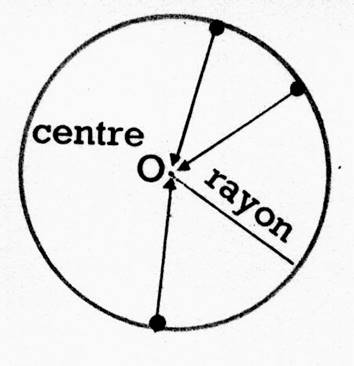
LE CERCLE . Tous les points du pourtour (on dit parfois la circonférence) d’un cercle, sont à égale distance d’un point qui est le centre du cercle. La distance du centre au pourtour est le rayon du cercle. On trace des cercles à l’aide d’un compas dont les pointes ont pour écartement la longueur du rayon.
Le cercle Le cercle est une ligne courbe .				Le disque Le disque est une surface !!! (voir dos 130 - 131)
TRAVAUX : EVALUATION
1.Tracez un cercle de 3 cm de rayon. Marquez plusieurs fois le rayon par des traits fins, mesurez ces traits sont-ils bien tous égaux ?
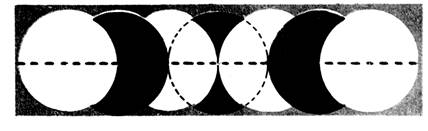
2 - A l’aide d’un compas, et sans changer de rayon, faites les dessins ci-dessous, en regardant bien où vous placez les centres des cercles.
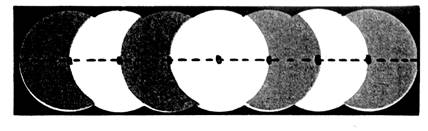
« A »					« B »
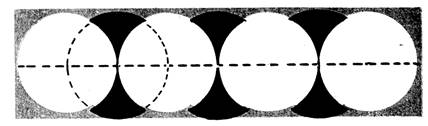
« C »					« D »
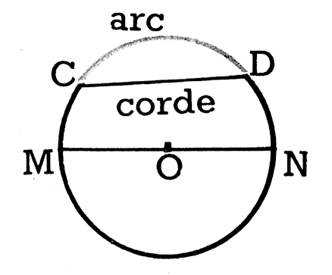
INFO cours :Un segment de droite (comme CD) qui joint deux points du pourtour s’appelle « corde ». Une portion du pourtour s ‘appelle « arc ». On dit que la corde CD sous-tend l’arc CD. Une corde qui passe par le centre s ‘appelle « diamètre du cercle » ; le diamètre mesure deux fois la longueur du rayon.
3 Dessinez et découpez un cercle. Pliez-le plusieurs fois en deux, afin de marquer des diamètres se coupent-ils bien tous au centre ? Sont-ils bien tous égaux entre eux ? Comment, sans mesurer, voir qu’ils mesurent chacun deux fois la longueur du rayon ?
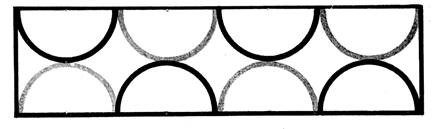
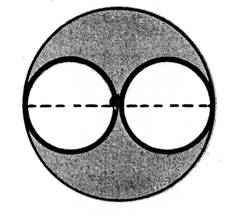
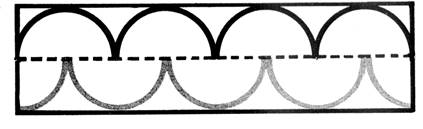
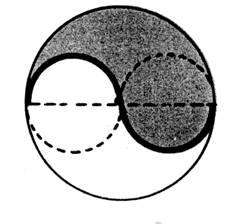
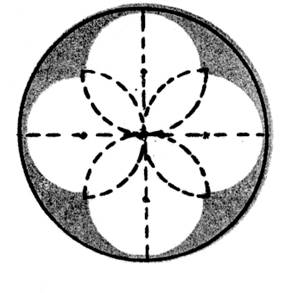
En repérant diamètres, centres, rayons, faites les dessins ci-dessous.
« A »		« B »
« C »		« D »
« E »	« F »