DOSSIER LE VECTEUR
PREPARATION du
CONTROLE:
REPONSES SOUHAITEES .
1°)ON
appelle "mesure" l'évaluation d'une quantité en la comparant à une
quantité déterminée.
2°)On
appelle "longueur" la dimension d'un objet linéaire de l'une à
l'autre de ses extrémités.
(l'unité de longueur est le mètre)
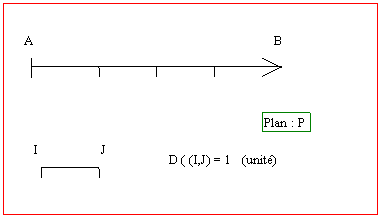
3°)On
appelle "distance" ,l'intervalle (ou les intervalles )qui existe
entre deux points ,ou deux objets.
(L'intervalle est généralement noté "u" associé à un segment
de droite d'unité "UN ")
4°)
Dans un bipoint ,si les deux points sont confondus ,il représente le vecteur
.."NUL"........ .
Il est
noté : 
5°)La
distance comprise entre l'origine et l'extrémité du bipoint s'appelle "NORME"
6°)Les caractéristiques d ' un vecteur sont :
Sa norme
Son sens
Sa direction
7°)Traduire
%Q
%Q : lire " norme du vecteur "
8°)Traduire en langage littéral :
"Si est le
représentant du (A,B), on peut écrire que :
%Q %Q = %Q 
%Q = d(A,B )
= mes. [AB]"
Si
le vecteur "vé" est le représentant du bipoint d'origine
"A" et d'extrémité "B", on peut écrire que la norme du
vecteur "vé" est égale à la norme du vecteur d'origine "A"
et d'extrémité "B" qui est
égale à la distance du bipoint
de "A" à "B" qui elle est égale à la mesure du
segment AB .
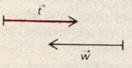
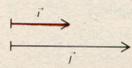
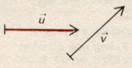
1°) Comparer les groupes
de deux vecteurs : sont-ils égaux ? pourquoi ?
|
Les vecteurs sont égaux .
|
|
|
Les deux vecteurs n’ont pas le même sens |
|
|
Les vecteurs sont égaux .
|
|
|
Les deux vecteurs sont de longueur
différentes :
|
|
|
Les deux vecteurs n’ont pas la même direction .
|
|
= 
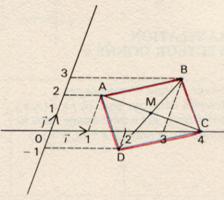
2°) Placer les points
A ( 1 ; 2 ) ; B ( 3 ;
3 ) ; C ( 4 ;0) ; D ( 2 ; - 1 ) dans un repère ( O ; 
; 
) . Montrer que ABCD est un parallélogramme .
|
|
|
AB ( 2 ; 1
) ; DC ( 2 ; 1 ) donc AB =
CD Conclusion : ( A , B , C , D ) ayant deux côtés opposés
parallèles et égaux est un parallélogramme. |
|
|
2e méthode : M milieu de
( A , C ) ; M ( N milieu
de ( B , D ) ; N ( Les diagonales se coupent en leur milieu. C.Q.F.D. |
|
, 1 )Soit
un vecteur donnez sa norme :
%Q
%Q= 4