WARMATHS

Les vecteurs

• Définition
• Vecteurs égaux
• Vecteur et parallélogramme
• Somme de deux vecteurs
• Composantes d'un vecteur
• Ce qu'il est utile de savoir faire
• Problème résolu

Voir aussi : translation, parallélogramme, repère

I Définition:

La notion de vecteur est étroitement liée à celle de translation.
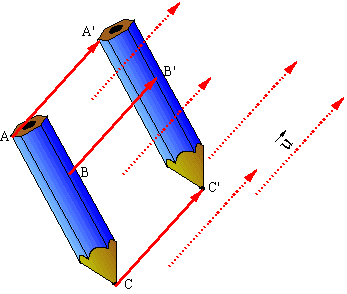
Une translation est définie dès que l'on connaît : la direction, le sens et la longueur du déplacement. Il s'agit d'un déplacement rectiligne, dans le plan, d'un objet donné. Chaque point de cet objet est déplacé sur la même direction, dans le même sens et de la même longueur.

La translation qui transforme A en A', transforme de la même façon B en B', C en C'. Ces points, reliés par une flèche indiquant le sens du déplacement, constituent une collection de couples : (A,A'), (B,B'), (C,C'). Tous les points de l'objet sont déplacés pareillement. Nous pouvons imaginer une infinité de flèches qui relient un point de l'objet à son image. Si cet objet se trouve lié à un autre objet (le crayon dans le cartable par exemple) qui subit la même translation, nous pouvons imaginer une infinité de flèches (en pointillés) qui relient tous les points de l'environnement à leur points images.

Cette infinité de couples définit un vecteur. Chaque couple est un représentant de ce vecteur. Et chaque représentant peut être dessiné à l'aide d'une flèche. 
Un vecteur est donc défini par: sa direction (le support de la flèche), son sens (le sens de la flèche) et sa longueur (la longueur de la flèche).

Dans la pratique, pour définir un vecteur il suffit d'indiquer l'un de ses représentants. Pour le nommer nous avons deux solutions:
- soit nous lui donnons un nom surmonté d'une flèche (pour préciser qu'il s'agit bien d'un vecteur et non pour indiquer son sens) comme indiqué sur la figure ci dessus : u surmonté d'une flèche toujours dirigée vers la droite de la lettre.
- soit nous choisissons l'un des couples et nous l'écrivons sans parenthèses et sans virgule, mais surmonté d'une flèche: et nous disons "vecteur AA', vecteur BB', ..." . Les points A, B, C.. sont les origines des représentants, les points A', B', C'... en sont les extrémités.

Remarque: la translation qui transforme A en A' est aussi appelée translation de vecteur

II Vecteurs égaux:

· Propriétés.

· Vecteur nul.

· Cas particulier: Milieu d'un segment

Les couples (A,A'), (B,B'), (C,C')... définissent des représentants d'un même vecteur. Nous pouvons choisir n'importe lequel de ces représentants pour donner un nom à ce vecteur.
Les notations désignant le même vecteur, nous pouvons écrire: Il s'agit d'une égalité vectorielle.

Propriétés:
- Si, par une translation, le point A a pour image le point B, et le point C a pour image le point D alors les vecteurs .

- .

Attention : la flèche au dessus du nom du vecteur est toujours orientée vers la droite de ce nom. Le sens du vecteur est donné de son point origine ( A par exemple) vers son point extrémité (A'). Les vecteurs ont des sens opposés : ce sont des vecteurs opposés. Ils ont la même direction, la même longueur mais pas le même sens.
De même des vecteurs qui n'ont pas la même direction, ou pas la même longueur, ne peuvent pas être égaux.

Vecteur nul :. le vecteur correspondant à un déplacement de longueur égale à 0 est appelé vecteur nul. On peut le noter, par exemple, .

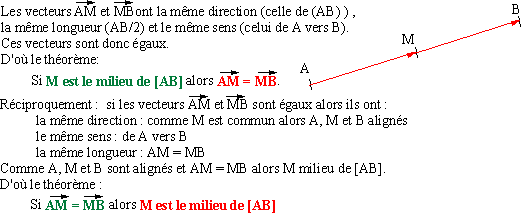
Cas particulier: soit M le milieu du segment [AB]

III Vecteurs et parallélogramme:

Rappels:

- Dans la translation qui amène A sur B, si C a pour image D alors ABDC est un parallélogramme.
Notez bien que A vers B et C vers D donne ABDC et non ABCD pour le nom du parallélogramme.

- Si ABCD est un parallélogramme alors , dans la translation qui amène A sur B, l'image de D est C.
Même remarque que ci dessus: attention à l'ordre des lettres dans le nom du parallélogramme. Sinon vous avez un quadrilatère croisé. Ceci est peut être plus facile à comprendre en utilisant la notation vectorielle ci dessous.

En passant aux notations vectoriels, ces théorèmes deviennent:

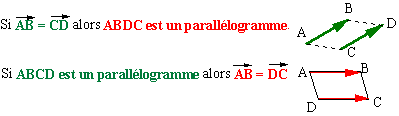
IV Somme de deux vecteurs:

· La somme de deux vecteurs est commutative

· Relation de Chasles

· Règle du parallélogramme

· Construction du vecteur somme

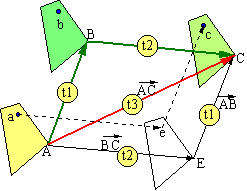
Soit la translation t1 qui amène le point A sur le point B et la translation t2 qui amène B sur le point C. Le résultat est la translation t3 qui amène A sur C. t3 est appelée translation composée de t1 suivi de t2
Nous allons démontrer que quelque soit le point a : si son image par t1 est b et que l'image de b par t2 est c alors l'image de a par t3 est c.

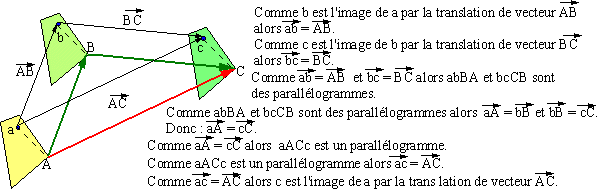
Donc c est l'image de a par t3.
Par définition : est le vecteur somme des vecteurs et .

Commutativité de la somme des vecteurs:

Nous allons montrer que l'ordre dans lequel s'effectue l'addition de deux vecteurs est sans importance. Un peu comme pour la somme de deux nombres (4+5=5+4 par exemple). Avec t2, de vecteur , nous pouvons translater A en un point E. Puis ce point E est translaté par t1, de vecteur , en un point que nous appellerons C'. Le vecteur est donc égal au vecteur . Comme = alors AECB est un parallélogramme. Comme AECB est un parallélogramme alors =. Ce qui signifie que C' est en C et que C est le translaté de E par t1 (de vecteur ). La somme des vecteurs et est encore .

Donc + =+ (cette propriété est appelée commutativité de la somme des vecteurs).

1. Relation de Chasles:

Par définition: la somme des vecteurs

Cas particulier :

2. Règle du parallélogramme:

Réciproquement:

3. Construction du vecteur somme:

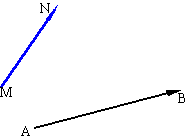
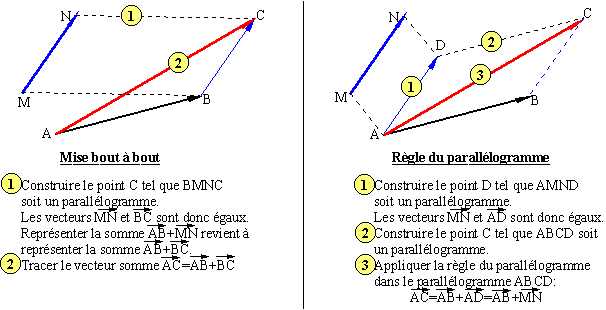
Soient deux vecteurs dont les représentants n'ont aucun point commun (pour avoir un cas général). Soient les vecteurs représentés par (M,N) et (A,B). Il y a deux façons de s'y prendre. Pour mener ces constructions à bien, il est nécessaire de savoir construire un parallélogramme à partir d'un côté et d'un point (ou de deux côtés consécutifs). Si vous avez quelques difficultés cliquez ici.

V Composantes d'un vecteur:

· Représentation d'un vecteur dans un repère.

· Calcul des composantes d'un vecteur

· Composantes de vecteurs égaux

· Composantes de la somme de deux vecteurs

1. Représentation d'un vecteur dans un repère:

Le plan est muni du repère d'axe (x'x) et (y'y), d'origine 0.
Soit les points A( x_A, y_A) et B( x_B, y_B). Le couple (A,B) représente un vecteur dessiné à l'aide d'une flèche d'origine A et d'extrémité B.
Les composantes de ce vecteur expriment les déplacements qu'il faut effectuer pour aller de A à B, en suivant des chemins parallèles aux axes.
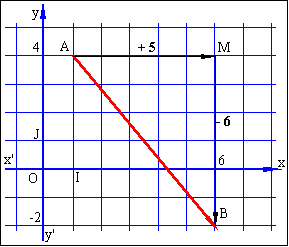
Exemple: A(1;4) et B(6;-2)

La première composante s'obtient en suivant , à partir de A, une ligne parallèle à (x'x), dans le sens positif (abscisses croissantes) ou négatif (abscisses décroissantes) selon la position de B. Nous arrêtons lorsque nous sommes à l'aplomb de B : pour notre exemple le point M. Pour aller de A en M nous augmentons les abscisses de 5. Ce qui donne la première composante : +5. La seconde composante s'obtient en suivant, à partir de M, une ligne parallèle à (y'y), dans les sens positif (ordonnées croissantes) ou négatif (ordonnées décroissantes) selon la position de B. Pour aller de M à B, nous diminuons les ordonnées de 6. Ce qui donne la seconde composante : -6.

Les composantes du vecteur sont notées (5 ; -6) comme pour les coordonnées d'un point. D'ailleurs le mot "coordonnées" est aussi utilisé pour désigner les composantes d'un vecteur.

1. Calcul des composantes d'un vecteur:

Exemple:
Reprenons l'exemple ci dessus: A(1;4) et B(6;-2).
En nous déplaçant parallèlement à (x'x) , pour aller de A à l'aplomb de B (point M) nous passons de l'abscisse 1 (celle de A) à l'abscisse 6 (celle de B). La première composante +5 est donc la différence entre l'abscisse de l'extrémité B et l'abscisse de l'origine A: (+6) - (+1) = +5.
De même pour la seconde composante. Nous passons de l'ordonnée 4 (celle de A ou de M) à l'ordonnée -2 (celle de B). La seconde composante -6 est donc la différence entre l'ordonnée de l'extrémité B et l'ordonnée de l'origine A : (-2) - (+4) = -6.
Plus généralement :
Si A( x_A, y_A) et B( x_B, y_B) alors les composantes du vecteur sont ( x_B - x_A ; y_B - y_A ).
Remarque:
Dans le calcul des composantes d'un vecteur, il faut toujours calculer:
1ère composante : abscisse de l'extrémité moins abscisse de l'origine.
2ème composante : ordonnée de l'extrémité moins ordonnée de l'origine.

2. Composantes de vecteurs égaux:

Si deux vecteurs sont égaux ils ne sont pas forcément représentés au même endroit dans le repère, mais ils sont, par définition :
de même direction (les droites qui supportent leurs représentations sont parallèles).
de même sens.
de même longueur.
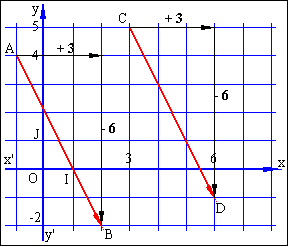
Exemple: soient les vecteurs et tels que A(-1;4), B(2; -2), C(3;5) et D(6;-1).

	Nous pouvons observer sur le dessin ci contre que les vecteurs et sont égaux. Calculons les composantes de ces vecteurs: (xB - xA ; yB - yA) = (2-(-1);-2-4) = (3;-6). (xD - xC ; yD - yC) = (6-3;-1-5) = (3;-6). et leurs composantes sont égales. Nous admettons que ceci est général et nous avons deux théorèmes très utiles:
Si deux vecteurs sont égaux alors leurs composantes sont égales. Si les composantes de deux vecteurs sont égales alors ces vecteurs sont égaux.

2. Composantes de la somme de deux vecteurs:

Soient les vecteurs   et . Nous avons :
(x_B - x_A ; y_B - y_A) et (x_C - x_B ; y_C- y_B)
et la relation de Chasles donne : += où (x_C - x_A ; y_C- y_A).
Si nous ajoutons à x_C - x_A la valeur 0=x_B - x_B et à y_C- y_A la valeur y_B- y_B nous ne changeons pas leur valeur:
x_C - x_A=x_C - x_A+x_B - x_B et y_C- y_A=y_C- y_A+y_B- y_B.
Ou, en écrivant autrement : x_C - x_A=(x_B- x_A)+(x_C - x_B), c'est à dire la somme des deux premières composantes des vecteurs et . De même:
En écrivant autrement : y_C - y_A=(y_B- y_A)+(y_C - y_B), c'est à dire la somme des deux secondes composantes des vecteurs et . D'où la règle:

La somme de deux vecteurs a pour composantes les sommes des composantes de ces vecteurs.

Exemple: soient (10;-5) et (3;4). 
Leur somme est (10+3;-5+4) =(13;-1).
Remarque: la démonstration ci dessus utilise deux vecteurs "bout à bout" (l'extrémité de l'un est l'origine de l'autre). Si ce n'est pas le cas, la règle s'applique encore car l'un des deux vecteurs peut être remplacé par un vecteur égal (donc de mêmes composantes) ayant comme origine, l'extrémité de l'autre.
Exemple: (-2;3) et (6;3). Calcul de +

Nous pouvons toujours construire le vecteur somme. Il suffit de représenter le vecteur par un vecteur égal (en pointillés rouges sur la figure) dont l'origine est l'extrémité de . Nous obtenons le vecteur =. Les composantes de sont les mêmes que celles de (-2;3). La somme + (en bleu) devient : +=+= dont les composantes sont les sommes des composantes de et . Nous calculons donc (-2+6;3+3)=(4;6). Donc (+)(4;6).(la somme est entre parenthèses pour éviter toute confusion).

VI Ce qu'il est utile de savoir faire:

1. Placer le translaté d'un point.

Avec la règle, l'équerre et le compas.
Exemple: soit trois points A, B et C. Placer les points D et E, translatés de C
a) par la translation de vecteur pour D.
b) par la translation de vecteur pour E.

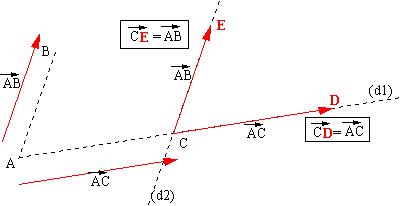
a) D étant le translaté de C par la translation de vecteur alors A, C et D sont alignés. Il suffit de prolonger la droite (AC) (droite (d1) ) et de porter avec le compas, à partir de C, la distance AC dans le sens A vers C.
b) E étant le translaté de C par la translation de vecteur alors = .
Comme = alors CEBA est un parallélogramme. Donc (CE) est parallèle à (AB). Il faut donc tracer une droite (2) parallèle à (AB) et porter sur (d2), à partir de C, la distance AB dans le sens de A vers B.

2. Représenter un vecteur dans un repère:

Nous avons trois cas:
a) nous connaissons les coordonnées des points du couple représentant le vecteur : il suffit de placer ces points !..
b) nous connaissons les composantes du vecteur: il existe une infinité de façons de représenter ce vecteur.

Exemple: soit le vecteur (-2;3). La figure ci dessous en donne plusieurs représentations.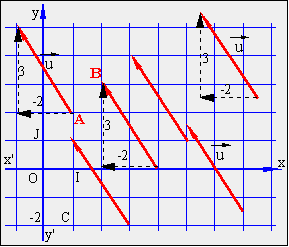

c) nous connaissons un point et les composantes du vecteur : une représentation particulière consiste à placer l'origine (l'extrémité) du vecteur au point connu et de placer son extrémité (origine) en utilisant les valeurs de ses composantes.
Exemples:
- placer un représentant de (-2;3) tel que A(1;2) soit l'origine. Voir la figure ci-dessus : en partant de A, nous devons aller "vers la gauche" de 2 unités (car première composante = -2) et aller "vers le haut" de 3 unités (car secondes composante = +3).
- placer un représentant de (-2;3) tel que B(2;3) soit l'extrémité. Voir la figure ci dessus: en partant de B, nous devons aller "vers le bas" de 3 unités et ensuite "vers la droite" de 2 unité. Dans ce dernier cas nous suivons le chemin opposé au cas précédent.

3. Lire les composantes d'un vecteur dans un repère:

Revoir, dans ce document, la définition des composantes.

4. Calculer les composantes d'un vecteur:

Revoir, dans ce document, le calcul des composantes.

5. Représenter la somme de deux vecteurs:

Revoir, dans ce document, la construction de la somme de deux vecteurs.

6. Calculer les composantes d'une somme de deux vecteurs:

Revoir, dans ce document, le calcul des composantes d'une somme de deux vecteurs.

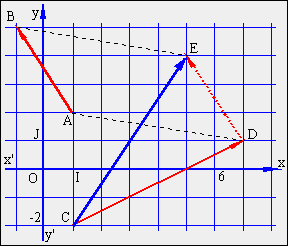
VII Problème résolu:

Ce problème permet de comprendre comment:

· calculer les composantes d'un vecteur.

· calculer les coordonnées d'un milieu

o en utilisant une formule

o en utilisant une égalité de vecteurs.

· calculer les coordonnées d'un point en utilisant une égalité de vecteurs.

· démontrer qu'un point est milieu d'un segment, avec une égalité de vecteurs.

· calculer les coordonnées d'un point translaté.

Note:

Pour tracer la figure vous pouvez utiliser Déclic. Une méthode de tracé est donnée à la fin du corrigé (voir le corrigé).

Énoncé:

Dans un repère orthonormal d'origine O.

1. Placer les points A(-1;2), B(4;1), C(6;4) et D sachant que ABCD est un parallélogramme.
2. Calculer les composantes du vecteur .
3. Calculer les coordonnées du point M, milieu de [AC].
4. Calculer les coordonnées du point D.

Soit E l'image de A par la translation de vecteur .

5. Démontrer que A est le milieu de [DE].
6. Calculer les coordonnées de E.