CORRIGE SOUSTRACTION de deux fractions de même dénominateur
CORRIGE CONTROLE: Objectif : QVI soustraction niveau.1
1°) La soustraction de deux
fractions (ou écriture fractionnaire ) n’est possible qu ’ à une condition :que les fractions aient le même
dénominateur.
3°)La traduction
en langage littéral de: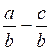 
=
est La soustraction de deux fractions de
même dénominateur est égale à une troisième fraction qui aura pour :Numérateur
la différence des numérateurs et pour Dénominateur le dénominateur commun.(En
utilisant d’autres
2°)Traduire en
langage mathématique de:
« La soustraction de deux
fractions de même dénominateur est égale à une troisième fraction qui aura pour
:Numérateur la différence des numérateurs et pour
Dénominateur le dénominateur commun. »est =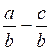
4°)Donner
la procédure permettant de faire la soustraction de deux fractions de même
dénominateur.
a) Identifier que les fractions ont le même dénominateur.
b)Faire la soustraction des numérateurs.
c)Etablir l’égalité dont le premier membre est la
soustraction de dépar et le deuxième membre est une
fraction dont le numérateur est la différence des numérateurs et le dénominateur le dénominateur
commun aux deux fractions.
CORRIGE :EVALUATION soustraction niveau.1
I
)
Effectuer les calculs suivants:
a)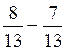
= 1/ 13 ;b)
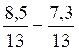= 1,2 / 13 ;c)
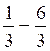= -5 / 3 ;d) 
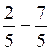= -5 / 5 ;e)
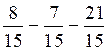= - 20 / 15
II:) Idem
a)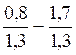
= -0,9 / 1,3 b)
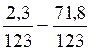= - 69,5 /123
III
)Faire
exercices avec des nombres décimaux
a)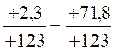
=
-69,5 / +123 ;b) 
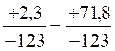= -69,5 /
-123 ;c)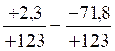
=
+74,1 / +123
IV Faire les additions suivantes
a)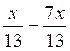
= - 6x /13 ;b)
=
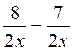1 / 2x
c)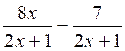 
=
(8x-7)/(2x+1)
Autres séries d’exercices
1° ) Faire les calculs suivants:
a)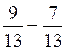 
=2 / 13 b ) 
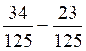=11
/ 125 c )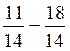 
= -7 / 14 ;(-1 /2)
2 °) idem
a )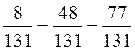 
=-117 /131
b )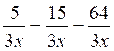 
=-74 / 3x
3°) Idem
a)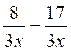 
= -9 /3x b) 
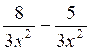=1 / x2
4°) Faire les soustractions suivantes : (pour pouvoir regrouper les termes en
numérateur il faudra revoir l’objectif
sur « Factoriser -
développer »
a )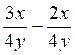 
=x / 4y
b )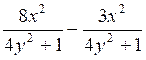 
=
5x2 / (4y2 +1)
c )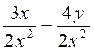 
= (3x-4y ) /2x2
d )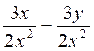 
=( 3 (x-y)) / 2x2
e )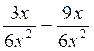 
= -1 /
x2