Auteur : WARME R.

INFORMATIONS  « LIVRE ».

Document neutre ; pour obtenir le livre interactif il faut posséder le code.

NOM : ………………………………

Prénom : …………………………..

Classe :…………………..

Année    scolaire : ………………………                                        

Dossier pris le : ……/………/………

Validation de la  formation :    O -  N

 Le : ……………………………………..

Nom du  formateur  : ……………………

ETABLISSEMENT : …………………………………………..

Devoir  exercices  sommatifs de(doit conclure le niveau)   niveau V entrée niveau IV.@

co@

Cette leçon est  très  importante. Elle doit être entièrement étudiée. Elle doit faire l’objet d’une attention toute particulière , elle est « particulièrement » longue à traiter ( il y a 4 règles fondamentales  à apprendre, dont une difficile à retenir,et il faut du temps pour apprendre ).

Chaque étape ( chapitre) doit être maîtriser .

Tous les chapitres doivent être entièrement maîtrisés.

La non maîtrise d’un seul de ses chapitres, risque d’entraîner  des  erreurs de calculs , « par ignorance », notamment lorsque l’on recherchera une valeur dans le cas d’une résolution d’équation ou lorsque l’on devra faire une  étude de fonction .

Cette leçon ,  demande du temps pour la comprendre , apprendre les règles et les utiliser ,  il est conseillé de travailler, en même temps ( en parallèle) ,une autre leçon en commençant par : ( voir la leçon n° 14 ) @

Leçon

Titre

N°6

COURS :  LES NOMBRES RELATIFS

(identifications et opérations).

 CHAPITRES :

1° ) les nombres relatifs (définition)  

Info Plus ! ! ! ! ! ! @

2°) Comparaison de nombres relatifs

Info Plus ! ! ! ! ! ! @

3°)Expression algébrique et somme algébrique 

Info plus ! ! ! ! ! ! @

4°) Les opérations avec les nombres relatifs :

INFO : Résumé ! ! ! @

  a) addition ;

Info Plus ! ! ! ! ! ! @

      b) soustraction ;

Info Plus ! ! ! ! ! ! @

         c) multiplication ;

Info Plus ! ! ! ! ! ! @

d) division

Info Plus ! ! ! ! ! ! @

5°) OPERATIONS  COMBINEES : Priorités dans les calculs.

C d :  ³info plus@

i1 9@ ;i 29@

I .  LE NOMBRE RELATIF .ou (les) nombres relatifs

@:i

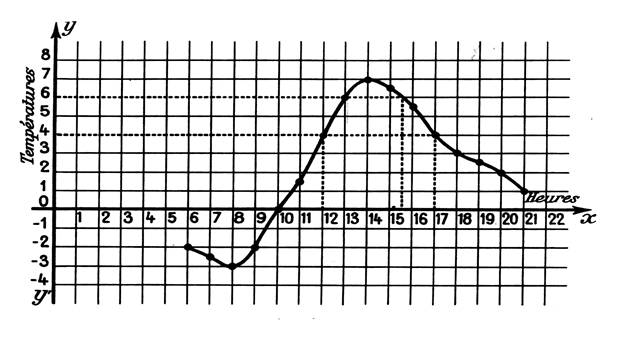
iinformations sur l’emploi des nombres relatifs :Dans la vie courante on utilise les nombres relatifs : pour exprimer une température ( +20°) . (voir les travaux en arithmétique) @ ( - 5°) ;

pour parler de son compte en banque ( je suis à   - 800 € ;ou je suis à + 800 € ) ; on entend à la radio que la bourse  (le CAC 40 ) a monté  de + 2,6% ; ou a baissé de  - 0,5% ,un plongeur  a plongé à  -12 m ; …. . Vous pouvez  trouver d’autres exemples.

Il faut apprendre à les reconnaître ces nombres relatifs  et faire des opérations avec ceux - ci .

Ci dessous , on a représenté dans le tableau les mesures de températures relevées au cours d’une journée.

On pourrait faire de même avec les notes obtenues par un élève , sur un mois de scolarité ;….

Trouvez des exemples …………….

Définition : Un alignement  horizontal de chiffres précédé d’un signe  + ou - , dans des parenthèses  est appelé : nombre relatif .

Commentaire :     Un nombre relatif peut être positif ou négatif !

Ne pas confondre , par exemple :                      ( - 5,38 )   et    ( + 5,38 ) .

Les nombres « opposés » @ : représentation graphique des nombres décimaux relatifs .

 La lettre  D ^-   désigne l’ensemble des nombres relatifs négatifs.

 La lettre  D ⁺   désigne l’ensemble des nombres relatifs positifs.

Déterminer sur la droite le  Lieu du point « A »  ( - 5,38 )    et  le lieu  du point « B »  ( + 5,38 )

On dit que ( - 5,38 ) et ( + 5,38 ) sont à l’opposé du zéro .

RESUME

Nombre relatif positif 

Nombre relatif négatif 

Définition :  Un alignement de chiffres  précédé  d’un signe « plus »  entre parenthèses  est un nombre  relatif positif .

Exemple :   ( +  35,7 )

Remarques :

La forme simplifiée d’un nombre relatif positif    ( +  35,7 )   est    + 35,7

Une simplification abusive, assimile « 35,7 »     à un nombre relatif .

Il est abusif d’écrire  que :

( +  35,7 )   = 35,7

Définition :Un alignement de chiffres  précédé  d’un signe « moins »  entre parenthèses est un nombre  relatif négatif .

Exemple : ( -  35,7 )

Remarques :

Exemple de simplification d’écriture :   - 35,7  est une simplification du nombre  relatif négatif ( -35,7).

i    Le nombre zéro est considéré à la fois comme « positif » et « négatif » .

Définition : Les nombres relatifs de signe contraire  sont dits : opposés.

Exemple 1 :                    (-3,7) et (+3.7) sont des nombres opposés

( info plus Cd : sur l’opposé d’un nombre ) @

Dans les nombres relatifs, l’alignement de chiffres séparés ou non par un virgule est  appelé  « la valeur absolue » du  nombre relatif .

Exemple 2 :  3,7  est la valeur absolue de  ( - 3,7 )  et de ( + 3 ,7 ).

RESUME DU VOCABULAIRE UTILISE

Nombres relatifs

Nombre relatif positif

Nombre relatif négatif

Forme simplifiée

Valeur absolue

( + 3,7)

( + 3,7 )

+ 3,7

3,7

( - 3, 7 )

( - 3,7 )

- 3,7

3,7

Attention ; Il ne faut pas confondre :

 le nombre décimal   3,7   avec le  nombre décimal  relatif  ( + 3,7 ) qui  lui a pour « valeur absolue »  la valeur  3,7

(En arithmétique  nous utilisons exclusivement des nombres décimaux ,En algèbre , nous utilisons exclusivement des nombres relatifs.   l’information sur le calcul à faire  et   l’utilisation des nombres « positifs » ou et des nombres relatifs est donnée par le  professeur ou dans l’énoncé

 i     On  ne devrait pas et on ne  peut pas assimiler le nombre  « 3,7 »  à la forme simplifiée  du nombre relatif  positif :  (+ 3,7)  .Ces deux  écritures désignent des nombres différents .Ils appartiennent à deux ensembles de nombres différents. @

SIMPLIFICATION @  D’ UN NOMBRE RELATIF @ 

Commentaire warmaths : ce chapitre est la cause de nombreuses erreurs de calculs en algèbre .  

Soit le nombre « positif »  :   ( +3)

                      Je peux simplifier un nombre relatif positif ,pour cela il suffit de supprimer les parenthèses et le signe   + se trouvant entre les parenthèses

      Ainsi  le nombre relatif positif   ( +3 ) devient  le nombre dit      "simplifié"     3    ;   mais attention danger , ce nombre sans signe porte le nom de « valeur absolue »  , et lors d’un calcul algébrique  il faut savoir transformer   « 3 »  en  (+3)  .

Autre exemple : dans une écriture algébrique  l’écriture   5,6   représente  en fait  le nombre relatif ( + 5,6)

Soit le nombre  négatif : ( -3) 

                                 Je peux simplifier un nombre relatif négatif  ,pour cela il suffit de supprimer les parenthèses et conserver le signe   -   se trouvant entre les parenthèses

Donc   ( -3 ) devient "simplifié"   -3    ; mais attention danger !   le signe  - n’est pas le signe de la soustraction .

Dans une expression algébrique   - 3  est en fait le nombre  relatif ( - 3 )  , devant lequel il est possible ( et conseiller )  de faire précéder ce nombre par le signe « + »

Ainsi de -3 on  écrit ( -3) pour conclure par l’écriture  + ( - 3)

C’est à dire  que :   - 7, 3   est en fait  le nombre relatif   ( - 7,3 )   qui peut être précédé par le signe +  ainsi   -7,3  est équivalent à l’écriture +( - 7,3)

Avant de travailler le chapitre suivant , observons deux cas ; 

1°)    Soit , par exemple , deux nombres relatifs :  ( - 2 )  et   ( + 3)  on peut  dire que :      Le  nombre (+3 ) est plus grand que le nombre (-2)

La valeur absolue « 3 »  du nombre  ( + 3 ) est plus grande que la valeur absolue « 2 »  du nombre ( +2)

2°) autre exemple : soit deux nombres relatifs :     ( - 5 )  et ( + 3) :

nous pouvons remarquer que :

    Le  nombre (+3) est plus grand que le nombre (-5)

    La valeur absolue « 5 »  du nombre  ( - 5  ) est plus grande que la valeur absolue « 3 »  du nombre ( +3)

    Le nombre ( + 3)  est plus grand que le nombre (- 5)

    Le nombre qui a la plus grande valeur absolue est le nombre ( -5)

    Le signe du nombre relatif qui a la plus petite valeur absolue est « + »

    Le signe du nombre relatif qui a la plus grande valeur absolue est  «  -  » 

i9  @

I I . COMPARAISON DE NOMBRES RELATIFS

Info Plus ! ! ! ! ! ! @

Définitions :

                        - Tout nombre relatif négatif est inférieur ou égal à zéro .

                        - Tout nombre relatif positif est supérieur ou égal à zéro .

                        - Un nombre relatif négatif est plus petit qu’un nombre relatif positif .

A )  Comparaison de deux nombres « négatifs » 

Règle : Si deux nombres relatifs sont négatifs , le plus petit est celui qui a la plus grande valeur absolue ; le plus grand est donc celui qui à la plus petite valeur absolue .

Exemple :  ( - 6 ) est plus petit que ( -2 ) , parce que  -6  est le plus éloigné de 0 sur une droite graduée .

( info plus Cd : voir repérage des nombres relatifs sur une droite @)

INFO : le signe    ±    signifie  « + » ou « - »  superposé  , il faut lire « plus ou moins » .

L’écriture ( ±  5 ) ; désigne à la fois le nombre ( +5) et le nombre ( -5) 

(Nota : ce signe est employé pour désigner la valeur de « x » , dans la résolution de  x ² )

Représentation graphique des nombres décimaux relatifs :

Sur  une droite graduée , sur laquelle on à placé un point d’abscisse « O » , on peut ranger les nombres relatifs et les lire dans un ordre croissant ou décroissant

Exemples : on donne   une série de nombres ordonnés

Non simplifiée :

(- 189) < (- 74) < (-  6)  < (- 5 )< (- 4) < (-2,3) < ( ±  0 ) < (+1)  < (+ 1,5) < (+ 5,9) < (+ 13) < ( (+ 147,34)

la même série « simplifiée » :

 - 189 < - 74 <-  6 < - 5 < - 4 < -2,3 <  0 < +1  < + 1,5 < + 5,9 < + 13 <  + 147,34

ou  bien

- 189 < - 74 <-  6 < - 5 < - 4 < -2,3 <  0 <   1  <  1,5 <  5,9 <  13 <   147,34

a) Classement par ordre croissant :

- 189 < - 74 <-  6 < - 5 < - 4 < -2,3 <  0 < +1  < + 1,5 < + 5,9 < + 13 < +147,34

Commentaires :   ( - 189)  est Le plus petit nombre , il est placé à l’extrême gauche de la ligne;  ( + 147 , 34)   est  le plus grand nombre , il est placé à l’extrême droite de la ligne

b) Classement  par ordre décroissant : 

+ 34  > + 15,6 > +3 > 0 > - 2 > - 3,4 > - 63 > - 137,8

Commentaires :   ( + 34 )  est Le plus grand  nombre , il est placé à l’extrême gauche de la ligne;  ( - 147 , 8)   est  le plus petit  nombre , il est placé à l’extrême droite de la ligne

En règle générale ,et  par habitude , on classe  du plus petit au plus grand , en partant de la gauche, en allant de la gauche vers la droite.

Comparaison de deux nombres « positifs »  « Info CD ici »  @)

La comparaison de deux nombres positifs ne doit pas poser de problème particulier , sinon retourner au cours N°1 . ( cours sur les nombres décimaux).
Rappel de la : Méthode  :

Le plus petit est celui qui a la partie entière la plus petite .

S’ils ont la  même partie entière  , on compare les parties décimales chiffre à chiffre à partir des dixièmes .

POUR CLASSER des nombres décimaux relatifs :

1°) il faut classer les nombres  positifs avec les positifs , les négatifs avec les négatifs ,

2°) Il faut classer,  pour chaque groupe, les  valeurs absolues ( il est souhaitable d' utiliser le tableau de numération) :

3°) ranger en fonction du signe

►Si les nombres sont positifs : on classe les valeurs absolues de la  plus petite à la plus grande en partant de la gauche.

►Si les nombres sont négatifs : on classe les valeurs absolues de la plus grande à la plus petite en partant de la gauche.

Exemple avec des nombres positifs  :

Enoncé : classer les nombres suivants (par ordre croissant) :

                         4,067   ; 4,07  ;  40,7  ;   4,071  ;  4,71   ;  4,701  ;  4,717  ; 4,08

Procédure:

a) « rentrer » les nombres dans le tableau de numération .

b)   compléter les cases "vides" avec des zéros

c)  dans le tableau donner un numéro d' ordre , lire les nombres à partir de l'ordre décimal le plus grand (ici les millièmes):

Partie entière  (multiples )

Partie décimale   (sous multiples)

Classe des millions

Classe des mille

Classe des unités

Dixièmes:

1^er ordre

décimal

Centièmes

2^ième ordre décimal

Millièmes

3^ième ordre

décimal

C

9^ième ordre

D

8^ième ordre

U

7^ème ordre

C

6^ième ordre

D

5^ième ordre

U

4^ième ordre

C

3^ième ordre

D

2^ième ordre

U

1^er ordre

0,1

ou

1/10

0,01

ou

1/100

0,001

ou

1/1000

Classement :

N°8

4

0

6

7

N°7

4

0

7

0

N°1

4

0

7

0

0

N°6

4

0

7

1

Quand les nombres sont placés , on numérote  les nombres dans l’ ordre  demandé.

N°3

4

7

1

0

N°4

4

7

0

1

N° 2

4

7

1

7

N°5

4

0

8

0

d) reporter le résultat:

Remarques :

Il y a deux solutions ( possibilités ) ou façons qui peuvent être  acceptées pour rendre compte du classement  :

a) les nombres sont classés et séparés par des points virgules :

            40,7 ;  4,717 ; 4,710 ;  4,701 ;  4,080 ; 4,071 ;  4,070 ;  4,067

b) les nombres sont classés et séparés par le signe   <   qui désigne une relation  dite « relation d’ordre »

          40,7  < 4,717 < 4,710 < 4,701 < 4,080 < 4,071< 4,070< 4,067

Autre méthode :  on demande de classer  les nombres suivants :  57,2 ; 57,23 ; 57, 236 ; 57,3 ; 57,235 ; 57,24

-  On classe par « rang décimal »  :   

                    On classe les parties entières  et puis  ensuite les parties décimales :

                                                                       57,2   et  57,3

       57,23  et  57,24

     57,235  et  57, 236

   On compare celui qui a le plus grand  nombre de dixième , à partie entière égale  : 

                                                        57,2  <  57,3

  On compare celui qui a le plus grand nombre de centièmes, à dixième égal   :

                                                     57,23 <  57,24

On compare celui qui a le  plus grand  nombre de  millièmes , à centième égal:

                                               57,235 < 57, 236

Remarques :  0,5  = 0,50 = 0,500

0,5

Lire "cinq dixièmes" d ' unité

0 ,50

Lire" cinquante centièmes" d ' unité

0,500

Lire " cinq cent millièmes d ' unité

*une "unité "vaut 1

ainsi : 57,2 = 57,20 = 57,200

On peut ainsi classer :

57,200  <57,230 <57,235 < 57, 236<  57,240<  57,300

(on peut « rajouter des « 0 » pour obtenir le même rang décimal , ce qui facilite la lecture des nombres « sous multiples » )

i9 @) 

III. transformations d’ écritures :EXpression algébrique et somme algébrique

Info plus ! ! ! ! ! ! @)

Ce chapitre est très important !!!!

iTrès souvent ,on vous donne en exercice  à faire des calculs  avec des nombres qui  sont écrits sous forme de nombres relatifs simplifiés. Cette suite de nombres séparée par des signes «  + , - ; …..)  est appelée   « communément » : expression algébrique.

 Il faut  transformer cette expression algébrique en une somme  algébrique ! ! ! ! !

On va voir , dans ce chapitre ,  que  les signes  « + et   -  » ne sont pas des signes « opératoires » .Ils indiquent  seulement si le « terme @)» est « positif » ou « négatif ».

Définition : Une suite de 2 ou plusieurs nombres précédés d’un signe + ou – sont appelée : expression algébrique .

Exemples : 

Attention : l’écriture :            « 12 + 6,5 »  devient  « + 12 + 6,5 »

Il en est de même   pour   « 14,5 – 53,7 »  se transforme  « + 14,5 – 53,7 » 

Ainsi : lorsqu ‘en tête d’expression il n’y a pas de signe, il faut  rajouter à l’expression le signe « + » en tête d’expression , avant de vouloir transformer une expression en somme algébrique.

Transformation des expressions algébriques en somme algébrique :

A )  Avec  2 nombres et   4 cas :

Dans les deux premiers cas il faut faire une première transformation:

1°)  « 12 + 6,5 » qui devient   « + 12 + 6,5 »   ;             on remarque : on a  dans l’ordre :deux nombres précédés du signe +

2°)  « 14,5 - 53,7 » qui devient   « + 14,5 – 53,7 » ;     on remarque : on a  dans l’ordre : un nombre précédé du signe + et un nombre précédé du signe - )

 3°)  « - 47 + 32 » ;           on remarque : on a  dans l’ordre : un nombre précédé du signe -   et un nombre précédé du signe +)

4°)  « - 30,2 – 8,34 » ;     on remarque : on a  dans l’ordre  deux nombres précédés qu signe -

Procédure de transformation d’une expression  algébrique en somme algébrique  

On retiendra que : pour transformer une expression  algébrique de deux nombres en somme algébrique  (addition de deux nombres relatifs)

Il faut : mettre le signe « + » en tête d’expression (si il n’y a pas de signe - ou de signe + ) puis il faut  mettre les chiffres et le signe qui les précède dans des parenthèses , pour terminer on sépare  les parenthèses contenant  ces nombres relatifs par le signe  + .

Application :

L’expression algébrique

Devient la somme algébrique :

L’expression algébrique

Devient la somme algébrique :

+12 +6,5

(+12) + (+6,5)

- 43,25 + 49

(- 43,25)+( + 49)

-47 + 32

(-47) +( + 32)

+ 14,5 – 53,7

(+ 14,5) +( – 53,7)

- 30,2 – 8,34

(- 30,2) +( – 8,34)

B )  Transformation d’une suite de nombre  (avec plus de 2 nombres)

Exemples  :    ►         - 7 – 3 – 23 

                     ►         3,2 – 4,67 – 5,63 + 14  qui devient    + 3,2 – 4,67 – 5,63 + 14 

L’expression algébrique

Devient la somme algébrique :

- 7 – 3 –23

(- 7) + ( – 3) + ( –23)

+ 3,2 – 4,67 – 5,63 + 14

(+3,2) + (– 4,67) + ( – 5,63) + ( + 14)

C )  Transformation d’une suite de nombre et  ou de  lettres  

Exemples  :    ►         - 7x – 3 – 23 

                     ►         3,2 – 4,67x – 5,63xy  + xyz  qui devient   + 3,2 – 4,67x – 5,63xy  + xyz 

Transformations :  

►         - 7x – 3 – 23   devient  la somme    (- 7x) + (– 3) + ( – 23)  

►          + 3,2 – 4,67x – 5,63xy  + xyz   devient (+ 3,2) +  (– 4,67x) + (– 5,63xy) + (+ xyz) 

Procédure de transformation d’une expression  algébrique en somme algébrique  

CAS GENERAL :

On retiendra que : pour transformer une expression  algébrique en somme algébrique  (addition de terme relatifs)Il faut  mettre le signe « + » en tête d’expression (si il n’y a pas de signe - ou de signe + ) puis il faut  mettre les chiffres (et ou  lettres)  et le signe qui les précède dans des parenthèses , et séparer  les parenthèses contenant  ces nombres relatifs par le signe +.

A quoi ça sert ??????? :

Pour factoriser , pour effectuer des calculs en algèbre ( pour résoudre ) , pour faire des calculs « apparemment »  simples avec des nombres positifs et  ou  négatifs , à chaque fois il faut  « identifier les termes »  et  les termes n’existent que dans la somme algébrique , aussi il faut savoir « impérativement » transformer les expressions  « algébriques » simplifiées :

+12 + 6,5 =  …(ce calcul est simple ) … ;  - 47 + 32 = ……(ce calcul est  moins simple ) ….. ; - 30,2 – 8,34  =………(ce calcul n’ est pas simple ) …. ; et ainsi de suite :

+ 14,5 – 53,7 = ……..;-43,25 + 49 = …….. ; - 7 – 3 –23  = …… ;3,2 – 4,67 – 5,63 + 14  = …………….;

Exemples de calculs qui deviennent simples :

Transformation : On veut effectuer une suite d’addition 

On calculera   la somme   :Voir cas par cas , dans la suite du cours , pour trouver le résultat

+12 + 6,5       =    (+12) + (+6,5) 

….de deux nombres positifs. (de  même  signe ).

- 47 + 32        =      (-47) + (+ 32) 

….de deux nombres de  signe contraire .

- 43,25 + 49   =   (- 43,25) + (+ 49) 

….de deux nombres de  signe contraire .

+ 14,5 – 53,7 =  (+ 14,5) + (– 53,7) 

….de deux nombres de  signe contraire .

- 30,2 – 8,34  =  (- 30,2) + (– 8,34) 

….de deux nombres  négatifs. (de  même  signe ).

Dans le cas ou il y a  plus de deux nombres :  on effectue toujours la transformation .parce que l’on veut  calculer une suite d’additions ! ! !

- 7 – 3 –23  = (- 7) + ( – 3) + ( –23) 

+3,2 – 4,67 – 5,63 + 14  = (+3,2) + (– 4,67) + ( – 5,63) + ( + 14) 

INFO PRATIQUE : Lorsqu’il y a plus de deux nombres , il faudra regrouper les nombres de même signe ( on fera la somme des nombres positifs , et la somme des nombres négatifs, pour conclure sur la somme de deux nombres de signe contraire .

i9  @)

IV ) LES  « 4 » OPERATIONS  simples avec les nombres relatifs :

INFO : Résumé ! ! ! @)

Commentaires :   Les groupes d’ opérations avec les nombres relatifs  sont au nombre de 3 :

                     Le groupe « addition » ( 3 règles)  ; le groupe de la multiplication ( 3 règles)    et le groupe de  la division ( 3 règles)  , on se souviendra que la soustraction « ne se fait pas » ( 1 règle) .

Ce qui en fait vous oblige à apprendre 10 règles pour réussir tous les exercices de calculs avec deux nombres relatifs.

i9   @)

IV.1                 Groupe :      ADDITION

Info Plus ! ! ! ! ! ! @)

Situations problèmes :

1°)  Sens que l’on peut donner à  une somme de 3,4 € :

En matière d’argent :

-          les recettes ou gains d’argent sont des « nombres arithmétiques » positifs , ils s’écrivent avec un signe +  dans des parenthèses. ( + 3,4 € )  ;

-           les dépenses ou dettes  sont des « nombres  arithmétiques » dits « négatifs » , ils s’écrivent avec un signe - dans des parenthèses. , ( -3,4 € )

Donc 3,4 € est une monnaie relative : je reçois 3,4 €  j’écris sur mon compte ( + 3,4) , de donne  3,4 € , sur mon compte j’écris  ( - 3,4) .

2°) Somme de nombres positifs :

Sur une journée je reçois : 2  €  et  5  € sur mon compte j’écris (+2) ;(+ 5) , je veux faire la somme j’écris : (+2)  +  (+ 5)  =  ( +  (  2 + 5 ) )

3°) Somme de nombres  négatifs  :

Sur une journée je donne  : 2  €  et  5  € sur mon compte je vais écrire (- 2 ) et (  - 5) , j’additionne ces deux valeur et j’obtient   (- 2)  +  (-  5)  =  ( -  (  2 + 5 ) )  = ( - 7 ) ; cela signifie que j’ai fait une dépense pour la journée de 7 €

4°) Somme de deux nombres de signe contraire : (somme d’une dépense et d’un gain ):

1^er cas : je n’ai rien en poche ;je dépense 2 €  et je reçois 5 € ; le bilan  est qu’il me reste 5 - 2 = 3  € , j’écrirai (+3) €  .

soit :   ( - 2 )  + ( +5 )  =  ( + ( 5 - 2 ) )   = ( + 3 )

2^ème  cas : j je n’ai rien en poche  je dépense 5 €  et je reçois 2 € ;

Bilan  je dois  5 - 2 = 3  € , j’écrirai (- 3) €

soit :   ( + 2 )  + ( - 5 )  =  ( - ( 5 - 2 ) )  = ( - 3 )

ce qui nous permet de généraliser :

¶ Addition de deux nombres de signe + 

Règle1: On énoncera :   Somme de deux nombres relatifs de signe  « + » :

       La somme de deux nombres relatifs de signe  « + »  est égale à un troisième nombre relatif qui aura pour signe  « le signe +   » et pour valeur absolue « la somme des valeurs absolues » .

Règle2:   On énoncera :  

Somme de deux nombres relatifs de signe  « - » :   La somme de deux nombres relatifs de signe  « - »  est égale à un troisième nombre relatif qui aura pour signe  « le signe -   » et pour valeur absolue « la somme des valeurs absolues » .

Règle 3  : On énoncera :  

La somme de deux nombres relatifs de signe  contraire   est égale à un troisième nombre relatif qui aura :

            - pour signe : « le signe  du nombre relatif qui a la plus grande valeur absolue  » 

            - pour  valeur absolue @): « la différence des valeurs absolues » . On soustrait    toujours  la plus grande valeur absolue  moins la plus petite valeur absolue ! ! !.

Pour additionner deux nombres de signe contraire  :

Le résultat est un nombre  qui aura pour signe , le signe  du nombre relatif qui à la plus grande  valeur absolue .

Exemple 1  :      ( + 6 ) + ( - 7 ) =          ( calcul « plus compliqué » si :    6 - 7  = ? )

Exemple 2   :          ( -  6 ) + ( +  7 ) =   ?   ( calcul « plus compliqué » si :    - 6 + 7  = ? )

i9   @)

IV.2                               SOUSTRACTION

Info Plus ! ! ! ! ! ! @)

Situations - problèmes :

Je suis à ma banque : j ‘ai   7 € à mon compte je vais retirer  3 € ; bilan :    ( +7 ) - ( +3) ; il me reste sur mon compte 4 € .

Je suis dans un magasin :j’ai 7 €  et que je dois   3 €    ;                 bilan :     ( + 7 ) + ( - 3 ) ;         il me reste    4 € .

je vois  et constate  que ( +7 ) - ( +3)   = ( + 7 ) + ( - 3 ) ,

On remarque que soustraire une valeur relative à un nombre relatif  c’est ajouter à ce nombre relatif l’opposé de cette valeur relative.

Pour deux nombres relatifs on trouvera  les quatre cas suivants :

( +7 ) - ( +3)   = ( + 7 ) + ( - 3 )    ;  ( =  + 4 )

( +7 ) - ( -3)    = ( + 7 ) + ( + 3 )    ; ( =  +10 )

( -7 ) - ( +3)      = ( - 7 ) + ( - 3 )    ; ( = - 10 )

( -7 ) - ( -3)       = ( - 7 ) + ( +3 )    ;  ( = - 4 )

A  chaque fois que cela est possible  on décidera de  transformer la soustraction ; pour calculer  on applique les règles de l’addition vu ci-dessus.

i1:  L’opposé @) de  ( + 3 ) est  ( -3) ; l’op. ( +7) = -7

i2: Avec les nombres relatifs, la soustraction ne se fait pas. @) On transforme cette soustraction.

Règle : On énoncera :   

Pour  soustraire un nombre relatif  ( 1)  à un autre nombre relatif  ( 2) , on ajoute  à (2) l’ opposé de (1) .

Ensuite : On applique  la règle de l’addition qui correspond aux  3 cas traités ci-dessus.

[un autre nombre relatif  ( 2)]  - [un nombre relatif  ( 1)    ] = nombre relatif  ( 2)]  + opposé du nombre relatif  ( 1) ] =

Exemple 1  :      ( + 6 ) -  ( - 7 ) =   ?          ( calcul pas possible !!!!! )

( pas de calcul immédiatement possible !)

Exemple 2 :      ( + 9 ) -  ( +11  ) =   ?          ( calcul pas possible !!!!! )     ( pas de calcul immédiatement possible !)

i n° 3   :  - 6  – 7   n’est pas une soustraction, mais l’addition de  ( - 6 ) + ( - 7 )

comme  6 – 7   n’est pas une soustraction mais l’addition  de ( + 6 ) + ( - 7 )

( revoir Info. : transformation d’une somme algébrique en somme algébrique @))

 i9 Info (notion)  @)

IV.3   MULTIPLICATION avec     2    D ^{+ ou -}

Info Plus 1 @)

La première règle sur la multiplication  est celle que l’on semble retenir le plus facilement , alors qu’il est compliquer d’expliquer pourquoi le produit de deux nombres relatifs de signe  - donne en résultat le signe « + » !!!!

Règle  1   : Le produit de deux nombres relatifs  de même signe , est égal à un nombre relatif qui aura  le signe    +  et qui aura comme valeur absolue, le produit des valeurs absolues .

Exemples :

 ( - 6 ) ( - 7 )  =   ( +  ( 6 7 ) )   =  ( + 42 ) ; forme simplifiée du résultat : + 42  ou 42

( + 6 ) ( + 7 )  =   ( +  ( 6 7 ) )   =  ( + 42 ) ; forme simplifiée du résultat : + 42  ou 42

Souvenez vous que le signe « multiplié » est sous entendu  entre deux parenthèses opposées

Règle  2   : Le produit de deux nombres relatifs  de signe contraire, est égal à un nombre relatif qui aura  le signe  -   et qui aura comme valeur absolue, le produit des valeurs absolues .

Exemples :

1°)  On multiplie un « négatif » par un « positif »

( - 6 )   ( + 7 )  =   ( -   ( 6 7 ) )   =  ( - 42 ) ; forme simplifiée du résultat : - 42

2°) On multiplie un « positif » par un « négatif ».

( + 6 )  ( -  7 )  =   ( -   ( 6 7 ) )   =  ( - 42 ) ; forme simplifiée du résultat : - 42

Dans le produit de deux nombres de signe contraire , le signe  « moins » l’emporte.

i9  Info (notions) @)

IV.4   DIVISION    avec     2 nombres    D ^{+ ou -}

Info Plus ! ! ! ! ! ! @)

Commentaire :       Pour effectuer la division de deux  nombres relatifs , on applique les mêmes règles des signes  que celles employées pour la multiplication .En ce qui concerne la valeur absolue du résultat , on calculera le quotient des deux valeurs absolues .

¶ Quotient de deux nombres relatifs  de même signe 

 Règle : Le quotient de deux nombres relatifs  de même signe  est égal à un nombre relatif qui aura  le signe  +  et qui aura comme valeur absolue  ,le quotient des valeurs absolues .

Exemples :

( - 42 ) + ( - 7 )  =   ( +  ( 42 :  7 ) )   =  ( + 6 ) ; forme simplifiée du résultat : +6

( + 24 ) + ( + 6 )  =   ( +  ( 24 : 6  ) )   =  ( + 4 ) ; forme simplifiée du résultat : +4

· Quotient de deux nombres relatifs  de signe contraire

Règle : Le quotient de deux nombres relatifs  de signe contraire est égal à un nombre relatif qui aura  le signe -   et qui aura comme valeur absolue, le quotient des valeurs absolues .

Exemples :

( - 42 ) + ( + 7 )  =   ( -   ( 42 :  7 ) )   =  ( - 6 ) ;   forme simplifiée du résultat :   - 6

( +24  ) + ( -  6 )  =   ( -   ( 24 : 6 ) )   =  ( - 4 ) ;   forme simplifiée du résultat :   - 4

¸ Simplification d’un nombre relatif

Positif :   ( +3)  Je peux simplifier un nombre relatif positif ,pour cela il suffit de supprimer les parenthèses et le signe   + se trouvant entre les parenthèses

      Donc   ( +3) devient "simplifié"   3    ; mais attention danger !il faut savoir faire l'inverse..

Négatif : ( -3)  Je peux simplifier un nombre relatif négatif  ,pour cela il suffit de supprimer les parenthèses et conserver le signe   -   se trouvant entre les parenthèses

      Donc   ( -3) devient "simplifié"   -3    ; mais attention danger !il faut savoir faire l' inverse..

Í   Fractions : (observer le signe des termes !!!!

        =   ( - (5 : 7)  )     ;      =   ( + ( 3 : 4 ) )     ;       =  ( -  ( 6,4 : 3 ))

              =      ;       =   ;      = ;     =

i9   @)

V) OPERATIONS COMBINEES : PRIORITES  de  CALCULS

C d :  ³info plus@)

iLes expressions algébriques  contiennent une  suite d’opérations , elles ne  contiennent pas de parenthèses :

¶ Suite d’additions

Exemple :  «   8 + 56 + 12 + 965,12 »   ( remarque : l’expression  ne contient que des « additions »:

Procédure 

Exemple

1^ere Etape

Transformer « l’expression » en « somme » de nombres relatifs

 x = «   (+8)+( + 56) + (+12) +(+ 965,12) »

2^eme Etape

Faire la somme des nombres de même signe

x = (  +  (8 + 56+12 + 965,12) ) 

à ce stade , il faut   faire la somme des valeurs absolues !!!

3^eme Etape

Rendre compte

x = (+1041,12)

· Suite de soustractions

i          Attention au signe du premier  nombre :

  + s’ il est négatif : faire la somme des nombres négatifs @)

 + s’il est positif :   faire la somme des nombres négatifs ; terminer par la somme de deux nombres de signe contraire@)

+          l’expression  débute par un signe «  -  »  et ne contient   que des signes « moins » .

 Exemple  « -12 - 56 - 4 - 5,7 » 

Procédure 

Exemple

1^ere Etape

Transformer « l’expression » en « somme » de nombres relatifs(SOS cours) @)

x = (-12) + (- 56) + (- 4) + (- 5,7) 

2^eme Etape

Faire la somme des nombres de même signe(SOS cours) @)

x = (- (12 + 56  + 4 + 5,7  ) 

3^eme Etape

Rendre compte

 x  = -12 - 56 - 4 - 5,7    = (-77,7)

+ L’expression  n’a pas de signe  en tête d’expression  ou  elle débute par un signe «  + »  et ne contient   que des signes « moins » .

Exemple : « 12-56-4-5,7 »    ou  « +12-56-4-5,7 »

Procédure 

Exemple

1^ere Etape

Transformer « l’expression » en « somme » de nombres relatifs(SOS cours) @)

x = (+12) + (- 56) + (- 4) + (- 5,7) 

2^eme Etape

Faire la somme des nombres de même signe(SOS cours) @)

(- (56  + 4 + 5,7  ) 

soit :     ( - 55,7 )

Somme des Valeurs absolues des nombres négatifs

3^eme Etape

Faire la somme des nombres de signe contraire

x =  (+12) + (- 55,7)

  = ( - ( 55,7 - 12 )

   =   (  - 33,7 )

4^emeEtape

 Rendre compte

12 - 56 - 4 - 5,7  = ( - 33,7 )

¸  L’expression  ne contient que  des « additions » et des « soustractions » .

Exemple :             x = - 12 + 56 - 4 + 5,7 

Procédure 

Exemple

1^ere Etape

Transformer « l’expression » en « somme » de nombres relatifs(SOS cours) @)

L’expression  algébrique  « x = - 12 + 56 - 4 + 5,7 »   devient la somme :

x = (-12) + (+56) + (-4) + (+5,7)

2^eme Etape

Regrouper les nombres de même signe

 (-12) ; (-4)  et (+5,7) ;(+56)

3^eme Etape

Faire la somme des nombres de signe contraire

(-(12+ 4 ))=    ( -16) 

(+(56 + 5,7 ))= ( +61,7)

4^emeEtape

Faire l'addition des deux sommes calculées (nombres de signes contraires)

x = (-16 ) + (+ 61,7 )

x = (+ ( 61,7 - 16 ) )

x = (+  45,7  )

5^emeEtape

Rendre compte

x = -12+56-4+5,7 

x = (+  45,7  )

¹ L’expression contient des multiplications :   (exemple :calcul d’un volume)

+  Il n’y a que des multiplications:  sans signe négatif 

Exemple     ( 91,2 6,9 )

Procédure: il faut faire le produit des nombres ( ou valeurs absolues)

Procédure

Exemple

1^ere Etape

1^ère multiplication :

91,2  = 10 ,8

2^eme Etape

2^ème multiplication

10,8 6,9 =  74,52

3^eme Etape

Rendre compte

91,2 6,9  = 74,52

Nombre impair @) de signe «moins » ,le produit  est « négatif » @)

+Il n’y a que des multiplications:  avec un ou des  signes négatifs  

Exemple :    ( - 91,2 6,9 ) ; ( - 9- 1,2 6,9 ) ; ( - 9-1,2 -6,9 ) 

Remarque :   Il faut faire le produit des nombres ( ou valeurs absolues)

Procédure

Exemple

1^ere calcul

1^ère  multiplication

( - 91,2 6,9 ) = ?

          - 91,2   devient    - 10,8

        et    - 10 , 8  6,9  =  - 74 , 52

2^eme calcul

          2^ème multiplication

( - 9- 1,2 6,9 )   = ? 

- 9- 1,2   devient     + 10,8

et             10,8 6,9 =  74,52

3^eme calcul

          3^ème multiplication

    ( - 9- 1,2  - 6,9 )   = ? 

- 9- 1,2   devient     + 10,8

et             +10,8  -6,9 =  - 74,52

4^eme Etape

On remarque :

Pour un nombre impaire de signe  -  donne un résultat négatif :

( - 91,2 6,9 )      =   -74,52

( - 9-1,2 -6,9 )   =    -74,52

Pour un nombre paire de signe  -  donne un résultat positif  :

( - 9- 1,2 6,9 )    =  +74,52

On retiendra que le  résultat d’une suite de produit  :

+ si la suite  de multiplications    à 1 ou 3 ; 5 ; 7 signes  « moins » : le résultat sera du signe « moins »

+ si la suite de multiplications  à 2 ; 4 ; 6 ; 8 ;…signes « moins » : le résultat sera du signe « plus » .

Remarques :

Si le nombre de  nombres est   impair @)  et de signe «moins » ,le produit  est « négatif » @)

Si le nombre de nombres est  pair @)  et de  signe « moins » ,  le produit   est positif .

On utilisera ce type de savoirs lorsque l’on devra calculer des  : x² ;   x  ³ ;  x ⁴ ; x ⁵ ; ….x ⁿ ,  si « x »  est un nombre relatif ,  on pourra déterminer le signe du résultat  avant d’effectuer le calcul.

Exemple : 

calcul de x ⁵   avec « x » = - 3 ; avant de calculer ,on sait par avance  que le résultat sera un nombre négatif.

+La suite de  multiplication ne contient que des nombres de signe négatif  

Exemple  (-9-1,2 -6,9 )

Procédure : calculer le produit des valeurs absolues ; compter le nombre de nombres .

si le nombre de nombres est  pair : le produit est un nombre relatif positif .

si le nombre de nombres est impaire : le produit est un nombre relatif négatif .

º La suite d’opérations ne contient que des divisions .( très rare)

Exemple : 15 : 8 :2

Remarque : Il faut commencer  par la division de gauche.

Procédure

Exemple

1^ere Etape

1^ère division :  15 : 8

1,875

2^eme Etape

2éme division :      1,875 : 2

0,9375

3^eme Etape

Rendre compte

15 : 8 :2 = 0,9375

Exemple :  Avec des fractions 

-          Vous avez travaillé le cours sur les opérations sur les fractions , alors vous avez  une première  réponse.

-           Vous n’avez pas travaillé le cours sur les fractions « opérations » alors faire comme il suit :

Le plus simple est d’écrire les fractions sous forme d’une division :

il faut commencer  par la division de gauche.

Procédure

Exemple

1^ere Etape

( :1,2 )

(13 : 7)  : 1,2 =   2,6 : 1,2 = 2,1666667

2^eme Etape

( : )

(13 :5) : ( 27 :8) =  2,6 : 3,375 = 0,7703703 

3^eme Etape

( : :1,2 )

[ (13 :5) : ( 27 : 8)] : 1,2 = 

    ( 2,6 : 3,375 )    : 1,2  =

         0,7703703    : 1,2  =     0,6419752

»  Suite d’opérations  contenant  que  des « multiplications » et des « divisions »

+ La division "tombe juste", la division représente un nombre décimal .

Exemple   :   ( 6216 : 51,2)

Procédure

Exemple

1^ere Etape

Faire la (ou les division) :

16 : 5 =  3,2

( 62 3,21,2)

2^eme Etape

Faire les multiplications :il n ' y a  pas d’ordre impératif à respecter ; 

mais il est conseillé  de faire les opérations  en partant de la gauche,

198,4 fois 1,2 = 238,08

3^eme Etape

Rendre compte 

:( 6216 : (1,2) =  238,08

+ La chaîne contient des "fractions ou écritures fractionnaires"

Exemple :            (621,2)

Une  division "ne tombe  pas juste" ;on dit aussi " la (ou les)division ne représente pas un nombre décimal ."

Procédure

Exemple

 1^ere Etape

Mettre la (ou les ) fraction sous forme d ‘une       fraction irréductible ou  d’une écriture décimale

 est irréductible ; et =0,6

2^eme Etape

 Mettre tous les autres nombres sous forme de fraction de dénominateur égal à 1

3^eme Etape

  Faire le produit des numérateurs sur le produit des dénominateurs

=

4^eme Etape

Laisser le résultat sous forme fractionnaire ,puis rendre irréductible la fraction

 ou » 86,357143

¼ La suite d’opérations   contient  des  additions, soustractions ,multiplications ,divisions

Exemple   :       -8,4  + 112 + 

Procédure :

Procédure