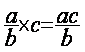Auteur : WARME R. INFORMATIONS : LIVRE. Document neutre ; il faut posséder le code pour accéder à la version interactive. (INITIATION : Conversion sexagésimal en décimal et vis à versa.)
NOM : ………………………………	Prénom : …………………………..	Classe :…………………..
Année scolaire : ………………………	Dossier pris le : ……/………/………	Validation de la formation : O - N Le : …………………………………….. Nom du formateur  : ……………………
ETABLISSEMENT : …………………………………………..

2/26	DOC : livre Elève .Cours interactifs - et travaux + corrigés.

Titre : FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.

DOSSIER N°2  COURS INTERACTIF : FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.

Information « TRAVAUX » Cliquer sur le mot « cours » !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU : Formation Niveau V (inclus le CAP et CFA)

OBJECTIFS : - Savoir identifier une fraction, savoir utiliser la fraction ; Ecrire une fraction sous forme décimale. - Savoir reconnaître et identifier des fractions égales. - Savoir multiplier une fraction par un nombre. - Savoir passer d’une Durée exprimée dans le système décimal dans un système sexagésimal et vis versa .

I ) Pré requis:

Division : (notion) @	.
Fraction : progression vue en primaire. @	.
Information sur La fraction en arithmétique. @	.
Fraction : unité. @	.
Pré requis : sur la fraction (pour niveau +++).@	.
Lecture : la fraction ( nomenclature). @	.

II ) ENVIRONNEMENT du dossier :

Index

Objectif précédent : 1°) les nombres. @

Objectif suivant : 1°) les 4 opérations@ Ensuite :les Opérations avec deux fractions. @ 3°) Valeur numérique d’une expression littérale@

1°) Tableau : @ 2°)Liste des cours @ 3°) les opérations sur les fractions . @ 4°) calcul numérique : la fraction. @

III ) LECON n° 2 :

FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.

Chapitres :		Travaux spécifiques : niv VI et V. @
Fraction	INFO 1 plus ! ! ! ! ! @	Dossier 138 - 139. @
Fraction décimale ; écriture décimale d’une fraction décimale et non décimale.	INFO 2 plus ! ! ! ! ! @	Dossier 150 @ et Dossier 151@
Fractions égales ( équivalentes)	INFO 3 plus ! ! ! ! ! @	Dossier 160 @et dossier 162 - 163@
Multiplication d’une fraction par un nombre	INFO 4 plus ! ! ! ! ! @	Dossier 158 @ et Dossier 159@
Calcul de durée ( système sexagésimal)	INFO 5 plus ! ! ! ! ! @	Dossier 173@

IV) INFORMATIONS «  formation leçon » :

		Travaux auto -formatifs		INTERDISCIPLINARITE : voir cas par cas ! !
Test	COURS	Contrôle	Evaluation : Travaux complémentaires : Série 1@ Série 2@ Série 3@	Sciences : - Les durées (n°1). @ - Calcul de temps ; de vitesse , de distance parcourue. @ - la vitesse uniforme. @	CORRIGE : @
			Travaux niveau VI et V sur les fractions Dos 138 - 139 @

V ) DEVOIRS ( écrits):

Devoir diagnostique L tests. @	Ÿ
Devoir Auto - Formatif ( intégré au cours) @	Ÿ
Devoir Formatif « Contrôle : savoir » ; ( remédiation) @	Ÿ
Devoir Formatif «  Evaluation  savoir faire » ( remédiation) @	Ÿ
Devoir sommatif. @	Ÿ
Devoir certificatif : ( remédiation )	Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Consignes :Travaux en « auto - apprentissage »

- Répondre sur feuille au « contrôle »

- Faire l’évaluation (écrire sur le document).

Lorsque ces travaux sont terminés demandez les corrigés. Comparez , corrigez , demandez des explications.

Validation : demander à ce que l’on vous remette le questionnaire du devoir,que vous passerez en salle. (pour le préparer ) 

Leçon	Titre
N°2 / 26	FRACTIONS – ECRITURE FRACTIONNAIRE - et DUREE

Chapitres :		Travaux spécifiques : niv VI et V
Fraction	INFO 1 plus ! ! ! ! ! @	Dossier 138 - 139@
Fraction décimale ; écriture décimale d’une fraction décimale et non décimale.	INFO 2 plus ! ! ! ! ! @	Dossier 150 @ et Dossier 151@
Fractions égales ( équivalentes)	INFO 3 plus ! ! ! ! ! @	Dossier 160 @et dossier 162 - 163@
Multiplication d’une fraction par un nombre	INFO 4 plus ! ! ! ! ! @	Dossier 158 @et Dossier 159@
Calcul de durée ( système sexagésimal)	INFO 5 plus ! ! ! ! ! @	Dossier 173@

Consignes :Travaux en « auto - apprentissage »

- Répondre sur feuille au « contrôle »

- Faire l’évaluation (écrire sur le document).

Lorsque ces travaux sont terminés demandez les corrigés. Comparez , corrigez , demandez des explications.

Validation : demander à ce que l’on vous remette le questionnaire du devoir,que vous passerez en salle. (pour le préparer ) 

COURS
	i9 @	1° ) Fraction	:i@

Cd ³ INFO 2 plus  ! @ Il y a « fraction »  si les deux nombres séparés par une barre sont des nombres entiers @ (noté : N ).
Exemples :	;  ; ; ….
Dans une fraction les deux nombres sont séparés verticalement : ► Le nombre « a » et « b » sont des nombres entiers. En tout état de cause il faut que le nombre « b » soit différent de zéro. @ ( noté : b ¹ 0 )		►« a » est le « numérateur » ► « b » est le « dénominateur »
► Dans le nombre entier « b » , nombre en dessous du trait de fraction ( appelé : dénominateur) indique en combien de parties égales on divise une quantité ( appelé : Unité) @
►► Dans le nombre entier « a » , nombre au dessus du trait de fraction ( appelé numérateur) indique combien on prend de ces parties .
Exemple : si on découpe l’unité 1 en 7 parts ; on peut écrire que Je prends 3 parts ; je prends les de 1 . On retiendra que est une fraction . A retenir : Ecritures qui sont considérées équivalentes ( équivalente signifie «  égale valeur » )  l’opération à faire est la « division » ( division = partage )

a : b					a ¸ b	a / b
i9 @		2°) Ecriture décimale d’une fraction décimale ; ou d’une fraction non décimale.								:i@
a) Ecriture décimale d’ une fraction décimale : Lorsque le dénominateur d’une fraction est 10 ; 100 ; 1000 ; …., nous avons ce que l’on appelle une fraction décimale (³) @ :
les fractions :				;  ;  ;			peuvent s’écrire sous forme d’une écriture décimale : 0,7 ; 0,23 ; 0,367 ; 0,4563 .
Une fraction est décimale si la « division tombe juste » . ( ³le quotient est exact ) @
b) Ecriture décimale d’une fraction « non – décimale » :
		Une fraction est dite « non – décimale » si la division ne tombe pas juste .( le quotient n’est pas exact ) : Exemple : trouver l’écriture décimale de :						► la division de 5 par 7 donne : 0,714285714285714285714285714285714 .(on pourrait continuer la division !)
► 5 / 7 n’a pas de valeur décimale exacte ; il faudra (³) « arrondir » @ pour donner un résultat et utiliser (³@) le signe « » » qui se lit «  presque égal à …. »
en conclusion , on peut écrire que 5 / 7 » 0,714 arrondi au millième près.
Remarques : ►On séparera la fraction et la valeur décimale arrondie par le signe « » » qui se lit «  peu différent de …. » ► La valeur décimale représentant la fraction non décimale est le quotient arrondi
i9 @			3°) Fractions égales ( équivalentes)								@ :i
iremarque : On ne peut pas additionner ou soustraire des fractions qui n’ont pas le même dénominateur, il faut transformer ces fractions pour pouvoir réaliser cette addition ou soustraction. La première étape est d’apprendre à trouver par le calcul une fraction égale ( équivalente) à une autre fraction . Pour vérifier si deux fractions sont égales il faut chercher à chacune sa valeur décimale !
Définition : Des fractions sont égales si elles ont la même écriture décimale .
		► on remarque que si l’on fait les divisions , on obtient le même quotient
Exemple : « est égale » à la fraction que l’on peut écrire  ; Parce que : 3 :5 = 0,6 et 24 : 40 = 0,6
Règle 1 : Si on multiplie le numérateur et le dénominateur d’une fraction par un même nombre , on obtient une fraction égale .
		Exemple : = =
Règle 2 : Si on divise le numérateur et le dénominateur d’une fraction par un même nombre , on obtient une fraction égale . ( Dans ce cas ,on dit que l’on simplifie la fraction @.)
		Exemple :					► on remarque que :12 est divisible par 2 ;3 ;4 ;12
Simplifier :
							►et que 24 est divisible par 2 ;3 ;4 ; 6 ; 8 ;12 ; 24
►Je peux donc diviser le numérateur et le dénominateur par 4 ; On a donc :
► On pourrait simplifier @ davantage ;et diviser de nouveau par « 3 »:							; ► 1 / 3 est une fraction dite « irréductible @». ( elle n’est plus divisible) @
A savoir : Une fraction est dite «  irréductible @» si elle ne peut plus être simplifiée.
Règle 3 : Pour transformer une fraction donnée (exemple ) en une fraction équivalente dont on impose (ou fixe) le dénominateur ( 100 ) : ( exemple : = ) On divise les deux dénominateurs ( exemple : 100 :5 = on obtient le quotient « 20 ») afin d’ obtenir le « quotient multiplicateur » , et l’on multiplie le premier dénominateur par le quotient calculé précédemment .
Exemple : On doit « Trouver » une fraction égale à et dont le dénominateur est « 100 » : ► J’ai « 5 » et je veux « 100 » : Pour obtenir le nombre « 100 » à partir du nombre « 5 » , il faut multiplier « 5 » par 20 . ( parce que 100 /5 = 20 )
		Je peux transformer la fraction 3/5 , et donner le dénominateur « 100 » On a donc
i9 @	4°) Multiplication d’une fraction par un nombre										:i@
1^ère règle : Pour prendre la fraction d’un nombre « c » on multiplie ce nombre « c » par le numérateur de la fraction « a » , puis on divise le résultat ( produit ) par le dénominateur.
	►Vous trouverez une explication sur « le pourquoi c’est comme cela  » lorsque vous étudierez « la multiplication de deux fractions ».
Exemple : énoncé : « Prendre » les de 24 : on en déduit de cet énoncé l’expression numérique (l’ opération) = 24 D’après la règle on calcule : 3 24 = 72 ;et puis on divise : 72 par 4 = 18

Règle 2 :Pour multiplier une fraction par un nombre , on peut calculer la valeur décimale de la fraction et multiplier cette valeur décimale avec le nombre.
On calcule le quotient de la division ( a : b = q ) et l’on multiplie ensuite « q » par le nombre « c ». Exemple : calculer les 3/4 de 24 ;
	Procédure :
	1°) Cet énoncé se traduit par l’expression numérique : 24
	2°) On calcule 3 : 4 ; ce qui donne 0,75
	3°) on calcule 0,75 24 = 18
	On remplace dans 24 ; par 0,75
Ce qui nous permet d’écrire que 24 = 0,75 24
Si l’on généralise on dira que : Pour multiplier une fraction par un nombre , on fait le produit de la valeur décimale de la fraction par ce nombre. Autre explication ; pour comprendre  : On doit se souvenir que :Le produit de deux fractions est égal à une « autre »fraction : - qui a pour « numérateur » le produit des numérateurs - et pour « dénominateur » : le produit des dénominateurs. Exemple : ( terminer le calcul)

Ce qui suit est donné POUR INFORMATION. !!!!!!!!!
i9 @		5°) Calcul de durée ( système sexagésimal et système décimal ) passage de l’un a l’autre .					:i@
		Pré requis info : « sur le Cd @ la Durée » Remarque : nous avons vu dans la leçon n°1 @ que pour classer et ordonner les nombres entiers et décimaux on utilise le système de numération décimale.
iOn peut exprime la durée en utilisant deux systèmes de numération du temps  : ►le système décimal : par exemple on dit  : trois heures et demi et l’on écrit 3,5h ; ou ► le système sexagésimal : par exemple :trois heures et demi s’écrit 3 h 30 mn Remarque : ce double système d’écriture et de lecture est aussi utilisé , pour exprimer la mesure des angles en degré . =Comme on dit indifféremment « une heure trois quart » est égale à « une heure quarante cinq minutes »  . ( 1 h 3/4 = 1,75 h = 1h 45 mn) La plupart du temps *: la durée est généralement exprimée en Heure ; minutes ; seconde .
	* Ce système de numération appelé « le système de numération sexagésimal » ( base :60)
	Dans le sport de haut niveau , on découpe la seconde en dix ; cent , voir mille . on a recours au chronomètre électronique pour mesurer des durées au dixième voir centième de seconde . (notamment en course automobile ; cyclisme , natation , 100 mètres à pied ...
	Abréviations et Symboles utilisés : « heure » à pour abréviation : h « minute » à pour abréviation min ; le symbole est …..’ (Signe appelé « slache » : ’ ) « seconde » à pour abréviation s le symbole est …… ’’ (Signe appelé « double  slaches ») Ainsi 2 heures 30 minutes et 15 secondes peut s’écrire dans le système sexagésimal : ► 2 h 30 min 15 s ► 2 h 30 ’ 15’’ Ainsi 2 heures 30 minutes et 15 secondes peut s’écrire dans le système décimal: ► 2 , 525 h
	Dans la vie quotidienne , il faut savoir passer d’un système à l’autre
	¶ Savoir passer du système sexagésimal au système décimal On peut passer du système sexagésimal ( exemple 1 h 30 min ) au système décimal ( devient :1,5 h : lire :une heure et demie ) :
Règle :Pour exprimer une durée @ dans le système décimal@ en prenant l’heure pour unité , on divise le nombre de minutes par 60 .
	Exemples :
	a) Exprimer 1 h 30 min dans le système décimal : ( l’heure étant l’unité) Procédure : - On remplace l’écriture 1h 30 min par l’ addition 1 h + 30 mn -On garde la partie entière « 1  heure » et l’on va diviser les 30 minutes par 60 ; 30 min par 60 , ( 30 : 60 = 0,5) - On peut alors écrire que 1 h + 30 mn ( forme sexagésimale en écriture simplifiée ) est égal 1 h + 30/ 60^ème d’heure ( forme sexagésimale en écriture non simplifiée ) soit 1 h + 0,5 h ( forme décimale non simplifiée). en conclusion : 1 h 30 min ( forme sexagésimale définitive ) = 1,5 h ( forme décimale en écriture définitive) en résumé :
	Durée exprimée avec le système sexagésimal		1 h 30 min	=	1,5 h	Durée exprimée avec le système décimal .
	b) (exemple 2) Exprimer 1 h 21 min ( écrit sous la forme sexagésimale) sous forme d’une écriture décimale . ( système décimal)  : Remarque : l’heure étant l’unité de base . Procédure : Si on divise « 21 » par « 60 » , on obtient « 0,35 » . En conclusion : 1 h 21 min = 1,35 h
	?Activité : transformer 1h 51’ = ? en valeur décimale. Autres exemples de transformation faisant intervenir des heures ; minutes secondes: ☺ 1h 35 min 25s = 1 + ( 35/60) + (25/3600) = 1 + 0,583 + 0,006 » 1, 6 h à 0,01 près ☺ 2 h 37 min 45 s = 2 + ( 37/60 ) + ( 45 /3600) = 2 + 0,6166 + 0,0125 » 2,6291 h à 0,00001 près
	· Savoir passer du système décimal dans le système sexagésimal.
	Règle :Pour exprimer la durée exprimée dans le système décimal dans le système sexagésimal , on multiplie la partie décimale par 60 pour obtenir le nombre de minutes.
	Exemple 1: Enoncé : Exprimer 1,6 h dans le système sexagésimal Procédure : - on décompose 1,6 h = 1 h + 0,6 h - on multiplie 0,6 par 60 : 0,6 60 = 36  ( 36’) ; donc 0,6 h = 0 h 36 min - on écrit : 1,6 h = 1h + 0,6 h = 1 h + 36 min
	Exemple 2 : Un trajet dure 2,70 h , exprimée cette durée en H et minutes .
	Procédure : - on décompose 2,70 h = 2 h + 0,70 h - on multiplie 0,7 par 60 : 0,7 60 = 42  ( 42 ’) ; donc 0, 7 h = 0 h 42 min - on écrit : 2,70 h = 2h + 0,7 h = 2 h + 42 min - conclusion le trajet durera 2heures et 42 minutes Activité : convertir en h, min ,s : 5,51 h ; 6,72 h  et 2,58 h ( nota : le problème se complique si nous avons une valeur décimale comprenant plus de deux chiffres ! ! voir sur le CD info plus!)

corrigé

5,51h = 5 h + 0,51 fois 60 = 5 h + 30,6 mn = 5 h + 30 mn + 0,6 fois 60 = 5h 30 mn + 36s

6,72 h = 6 h + 0,72 fois 60 = 6 h + 43,2 mn = 6 h + 43 mn + 0,2 fois 60 = 6 h + 43 mn + 12s

2,58 h = 2 + 0,58 fois 60 = 2 h + 34,8 mn = 2 h + 34 mn + 0,8 fois 60 = 2 h + 34 mn + 48 s

ETUDE N°2

Demander @ les TRAVAUX d ’ AUTO - FORMATION sur : FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.